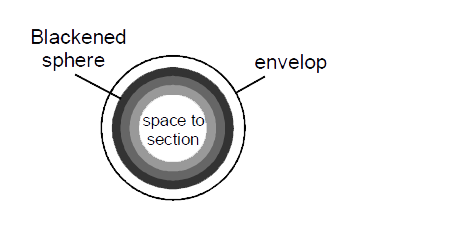
The shell of a space station is a blackened sphere in which a temperature T = 500K is maintained due to operation of appliances of the station. Find the temperature of the shell if the station is enveloped by a thin spherical black screen of nearly the same radius as the radius of the shell.

Find out energy stored in the electric field of uniformly charged thin spherical shell of total charge Q and radius R.

The ratio of the radii of gyration of a spherical shell and solid sphere of the same mass and radius about a tangential axis is

A force F acts at the centre of a thin spherical shell of mass m and radius R. Find the acceleration of the shell if the surface is smooth.

A tangential force F acts at the top of a thin spherical shell of mass m and radius R . Find the acceleration of the shell if it rolls without slipping.

By virtue of some internal mechanism, temperature of spherical shell is maintained in steady state which emits radiation like black body while kept in vaccum and isolated from all radiation. If this shell is enveloped by another shell B of same radius, still emitted like a black body, find the ratio of temperatures of shell B and shell A when it was alone:

Find the self gravitationl potential of (a) a thin unifrom spherical shell of radius R snd mass M, (b) a solid sphere of the same radius and mass .

A very thin metallic shell of radius r is heated to temperature T and then allowed to cool. The rate of cooling of shell is proportional to

A small sphere (emissivity =0.9, radius =r_(1) ) is located at the centre of a spherical asbestos shell (thickness =5.0 cm , outer radius =r_(2) ) The thickness of the shell is small compared to the inner and outer radii of the shell. The temperature of the small sphere is 800 K while the temperature of the inner surface of the shell is 600 K The temperature of small sphere is maintained constant. Assuming that r_(2)/r_(1)=10.0 and ignoring any air inside the shell, find the temperature (in k) of the outer surface of the shell Take : K_(asbestor)=0.085 W//m^(@) C sigma = 17/3 xx10^(-8) W//m^(2)k^(4)