A uniform solid cone of mass m, base rad...

A uniform solid cone of mass m, base radius ‘R’ and height 2R, has a smooth groove along its slant height as shown in figure. The cone is rotating with angular speed `omega`, about the axis of symmetry. If a particle of mass ‘m’ is released from apex of cone, to slide along the groove, then angular speed of cone when particle reaches to the base of cone is

Similar Questions

Explore conceptually related problems

If the base radius and height of a right circular cone are 28dcm. And 21dcm., then the slant height of the cone is

When a cone is opened along its slant height, it gets the shape of a

A cone has a slant height of 8 and a lateral area of 48pi . What is the radius of the base of the cone ?

A wheel of moment of inertial I and radius R is rotating about its axis at an angular speed omega . It picks up a stationary particle of mass m at its edge. Find the new angular speed of the wheel.

A wheel of moment of inertia I and radius R is rotating about its axis at an angular speed omega . It picks up a stationary particle of mass m at its edge. Find the new angular speed of the wheel.

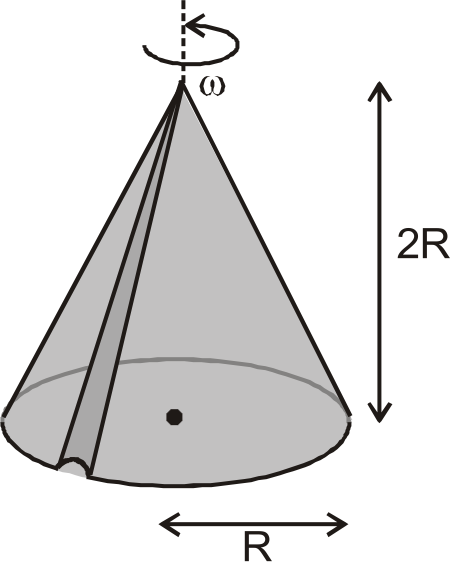
From a uniform solid cone of base radius R and height H, a symmetric cone of the base radius (R)/(2) is removed as shown. Then the centre of mass is shifted by H/n. Find the value of of n.

From a hemisphere of radius R a cone of base radius R/w and height R is cut as shown in figure. Find the height of centre of mass of the remaining object.

If a solid sphere of radius r is melted and cast into the shape of a solid cone of height r, then the radius of the base of the cone is

Similar Questions

Recommended Questions