Similar Questions
Explore conceptually related problems
Recommended Questions
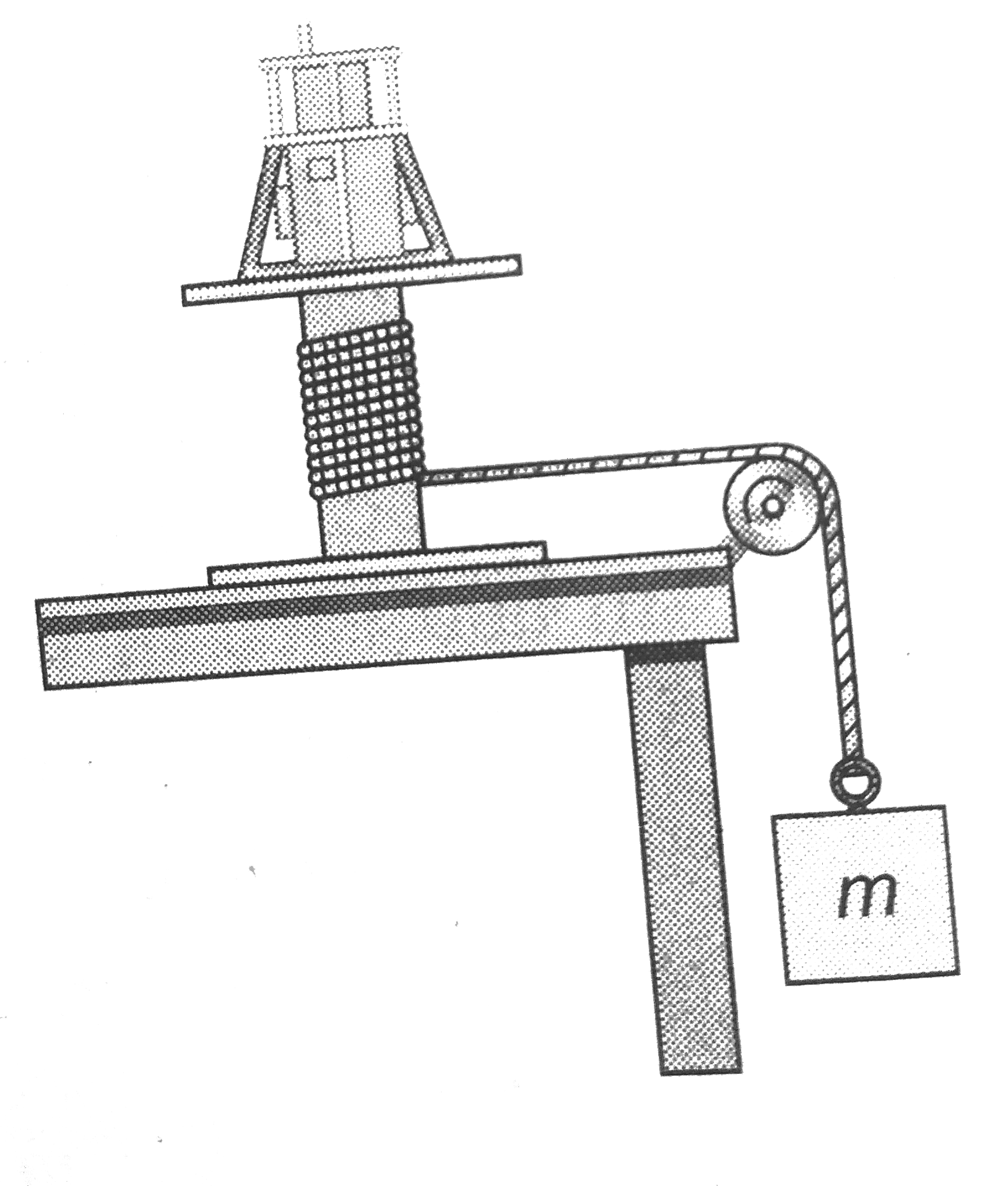
- Figure shows a counterweight of mass m suspended by a cord wound aroun...
Text Solution
|
- A stationary light, smooth pulley can rotate without friction about a ...
Text Solution
|
- A uniform spherical shell of mass M and radius R rotates, about a vert...
Text Solution
|
- Figure shows a counterweight of mass m suspended by a cord wound aroun...
Text Solution
|
- The coefficient of static friction between a small coin and the surfac...
Text Solution
|
- (i) A child stands at the centre of turntable with his two arms out st...
Text Solution
|
- A coin kept at a distance of 5 cm from the centre of a turntable of ra...
Text Solution
|
- संलग्न चित्र में R त्रिज्या की डिस्क का एक चौथाई भाग दिखाया गया है। इ...
Text Solution
|
- (a) A child stands at the centre of a turntable with his two arms outs...
Text Solution
|
 .
.