Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
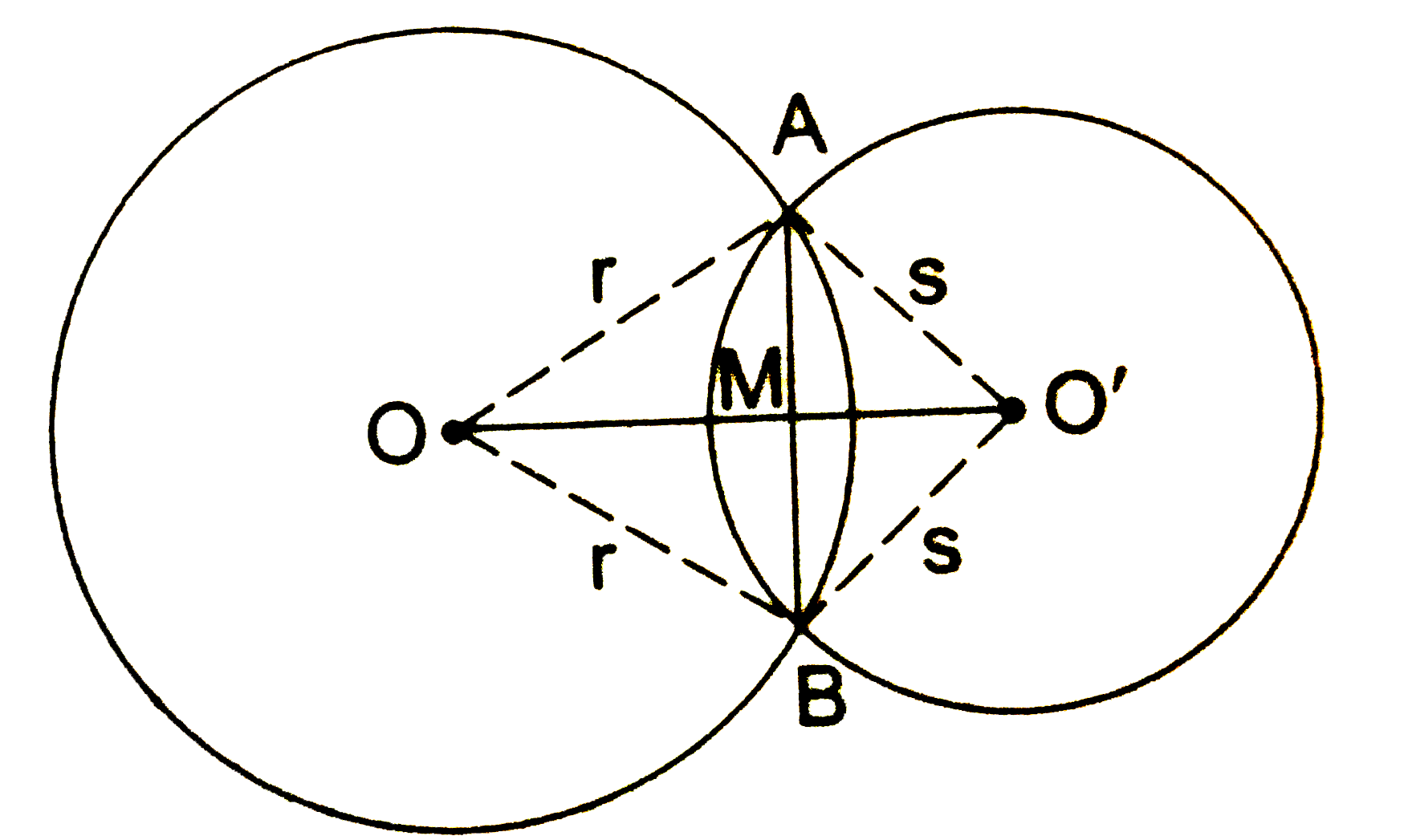
- If two circles intersect at two points, prove that their centres lie ...
Text Solution
|
- If two circles intersect at two points, prove that their centres lie ...
Text Solution
|
- If two circles intersect in two points, prove that the line through th...
Text Solution
|
- If two circles intersect in two points; prove that the line through th...
Text Solution
|
- Theorem :-2 The perpendicular from centre of a circle to the chord bis...
Text Solution
|
- Two circles itnersect each other in two points. Prove that the line th...
Text Solution
|
- यदि दो वृत्त एक-दूसरे के दो बिन्दुओ पर प्रतिच्छेद करते हो, तो सिध्द की...
Text Solution
|
- यदि दो वृत्त एक-दूसरे को दो बिंदुओं पर प्रतिच्छेद करते हैं तो सिद्ध क...
Text Solution
|
- If two circles intersect at two points, prove that their centres lie o...
Text Solution
|