Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
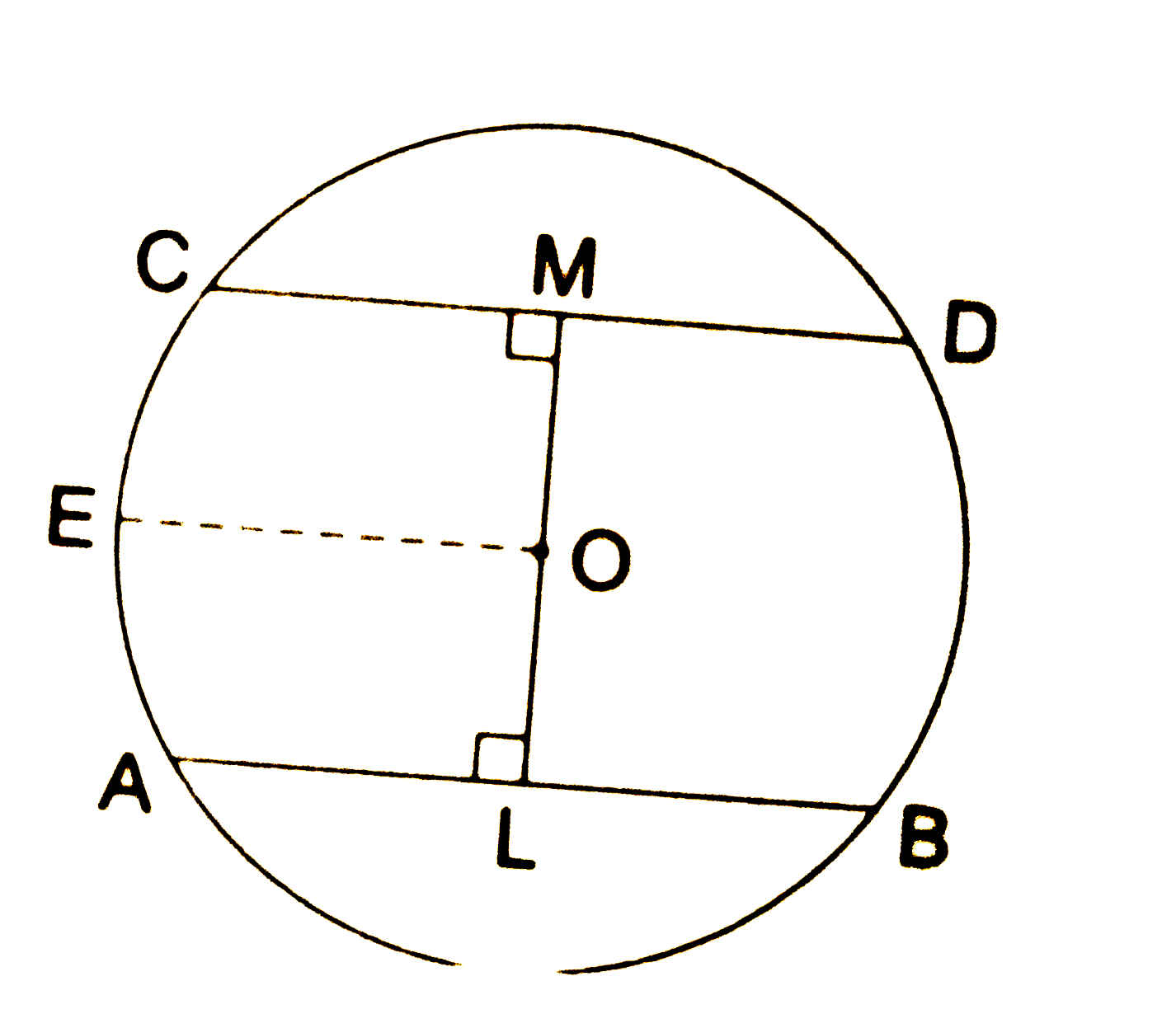
- Prove that the line joining the mid-points of two parallel chords of a...
Text Solution
|
- Prove that the line joining the mid-points of two parallel chords of a...
Text Solution
|
- prove that the line joining the mid-point of two equal chords of a c...
Text Solution
|
- Prove that the line joining the mid-point of a chord to the centre ...
Text Solution
|
- If a line segment joining mid-points of two chords of a circle passes ...
Text Solution
|
- Prove that the line segment joining the points of contact of two paral...
Text Solution
|
- सिद्ध कीजिए की एक वृत्त की दो समान्तर जीवाओं के मध्य बिन्दुओं को मिलान...
Text Solution
|
- सिध्द करो कि किसी वृत्त की दो समानान्तर जीवाओ के मध्य-बिन्दुओ को मिलान...
Text Solution
|
- सिध्द करो की वृत्त की किसी जीवा के मध्य-बिंदु को वृत्त के केंद्र से मि...
Text Solution
|