Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
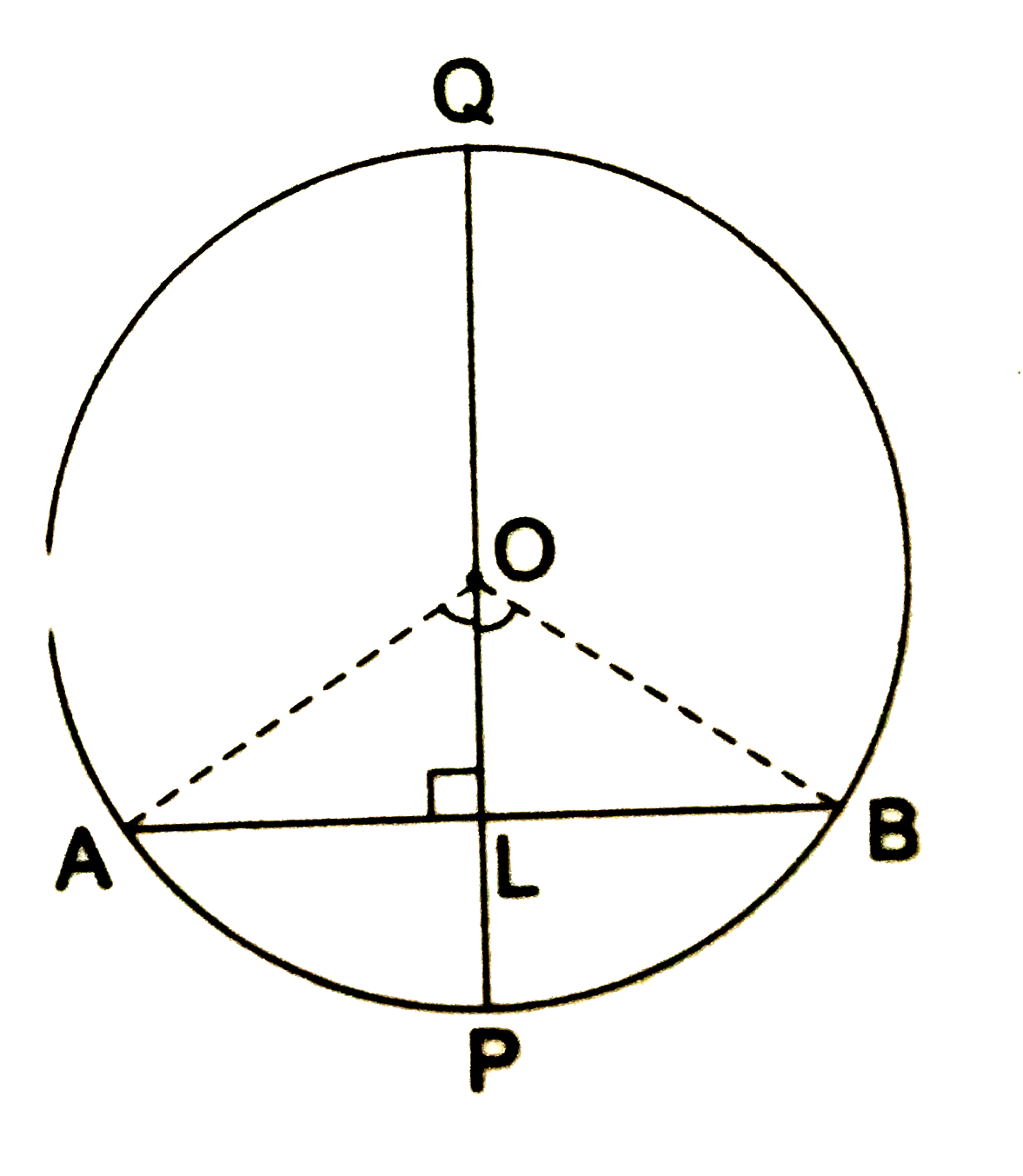
- Prove that the right bisector of a chord of a circle, bisects the co...
Text Solution
|
- Prove that the right bisector of a chord of a circle, bisects the c...
Text Solution
|
- If a diameter of a circle bisects each of the two chords of a circle, ...
Text Solution
|
- A chord PQ of a circle is parallel to the tangent drawn at a point R o...
Text Solution
|
- If a diameter of a circle bisects each of the two chords of a circle...
Text Solution
|
- Prove that the right bisector of a chord of a circle, bisects the ...
Text Solution
|
- Prove that a diameter of a circle which bisects a chord of the circ...
Text Solution
|
- If the perpendicular bisector of a chord AB of a circle PXAQBY interse...
Text Solution
|
- If two chords AB and CD of a circle AYDZBWCX intersect at right angles...
Text Solution
|