Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
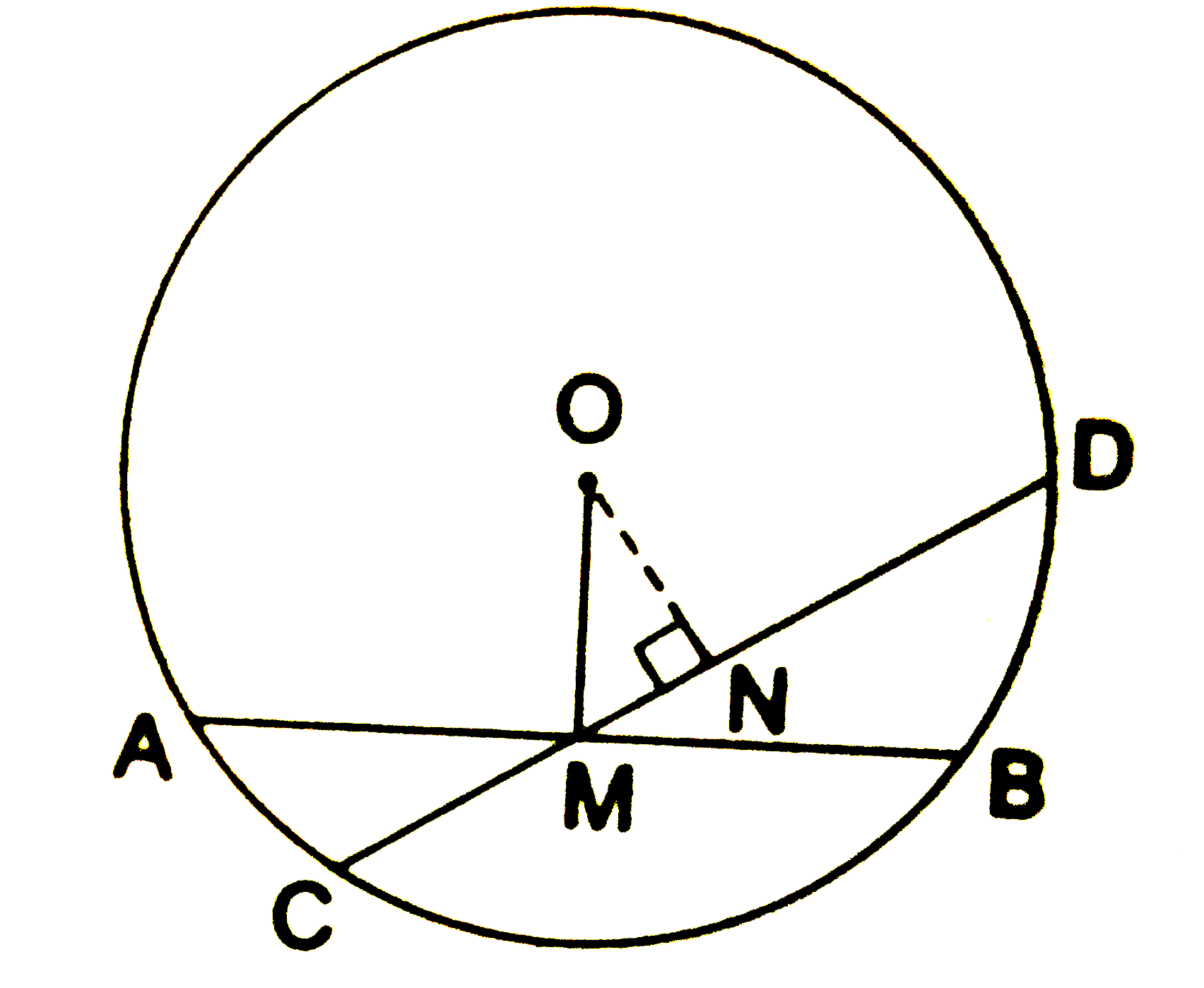
- Prove that all the chords of a circle through a given point within it,...
Text Solution
|
- Prove that all the chords of a circle through a given point within it,...
Text Solution
|
- In two concentric circle, prove that a chord of larger circle which is...
Text Solution
|
- Prove that a diameter AB of a circle bisects all those chords which ar...
Text Solution
|
- Prove that in two concentric circles, the chord of the larger circle w...
Text Solution
|
- Write with proof which of the chords passing through any point ...
Text Solution
|
- सिध्द करो कि किसी वृत्त के अंदर स्थित किसी दिए गए बिन्दु से गुजरने वाल...
Text Solution
|
- Prove that in two concentric circles, the chord of the larger circle,...
Text Solution
|
- Prove that a diameter AB of a circle bisects all those chords which ar...
Text Solution
|