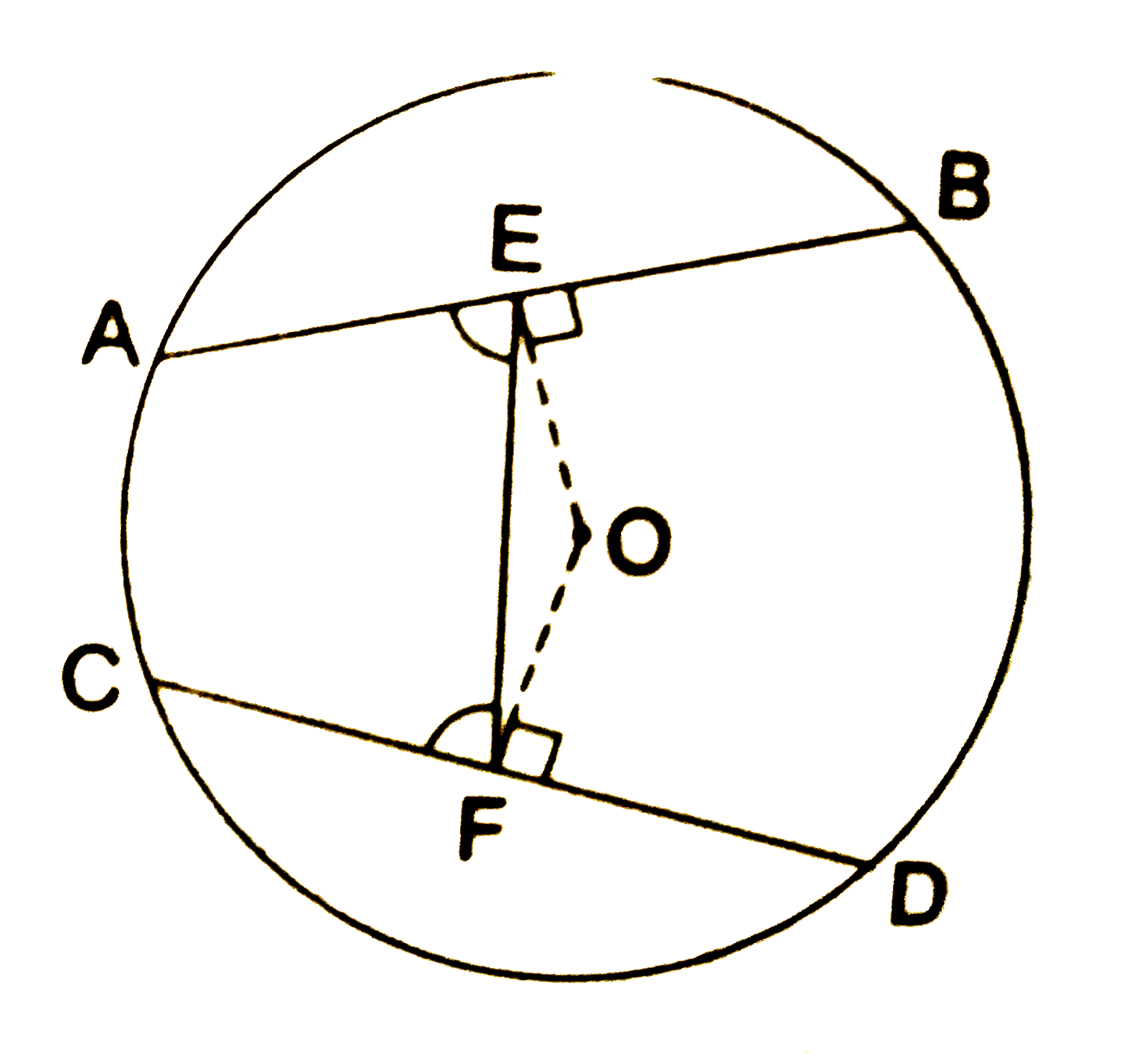
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- prove that the line joining the mid-point of two equal chords of a ...
Text Solution
|
- If two equal chords of a circle intersect within the circle, prove th...
Text Solution
|
- Prove that if chords of congruent circles subtend equal angles at the...
Text Solution
|
- If the angles subtended by two chords of a circle at the centre are ...
Text Solution
|
- prove that the line joining the mid-point of two equal chords of a c...
Text Solution
|
- If the angle subtended by two chords of a circle at the centre are equ...
Text Solution
|
- सिद्ध कीजिए कि यदि सर्वांगसम वृत्तों कि जीवाऍ उनके केन्द्रो पर बराबर क...
Text Solution
|
- यदि एक वृत्त की दो समान जीवाऍ वृत्त के अंदर प्रतिच्छेद करे, तो सिद्ध क...
Text Solution
|
- सिद्ध कीजिए कि एक वृत्त की दो बराबर जीवाओं के मध्य बिन्दुओं को मिलाने ...
Text Solution
|