Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
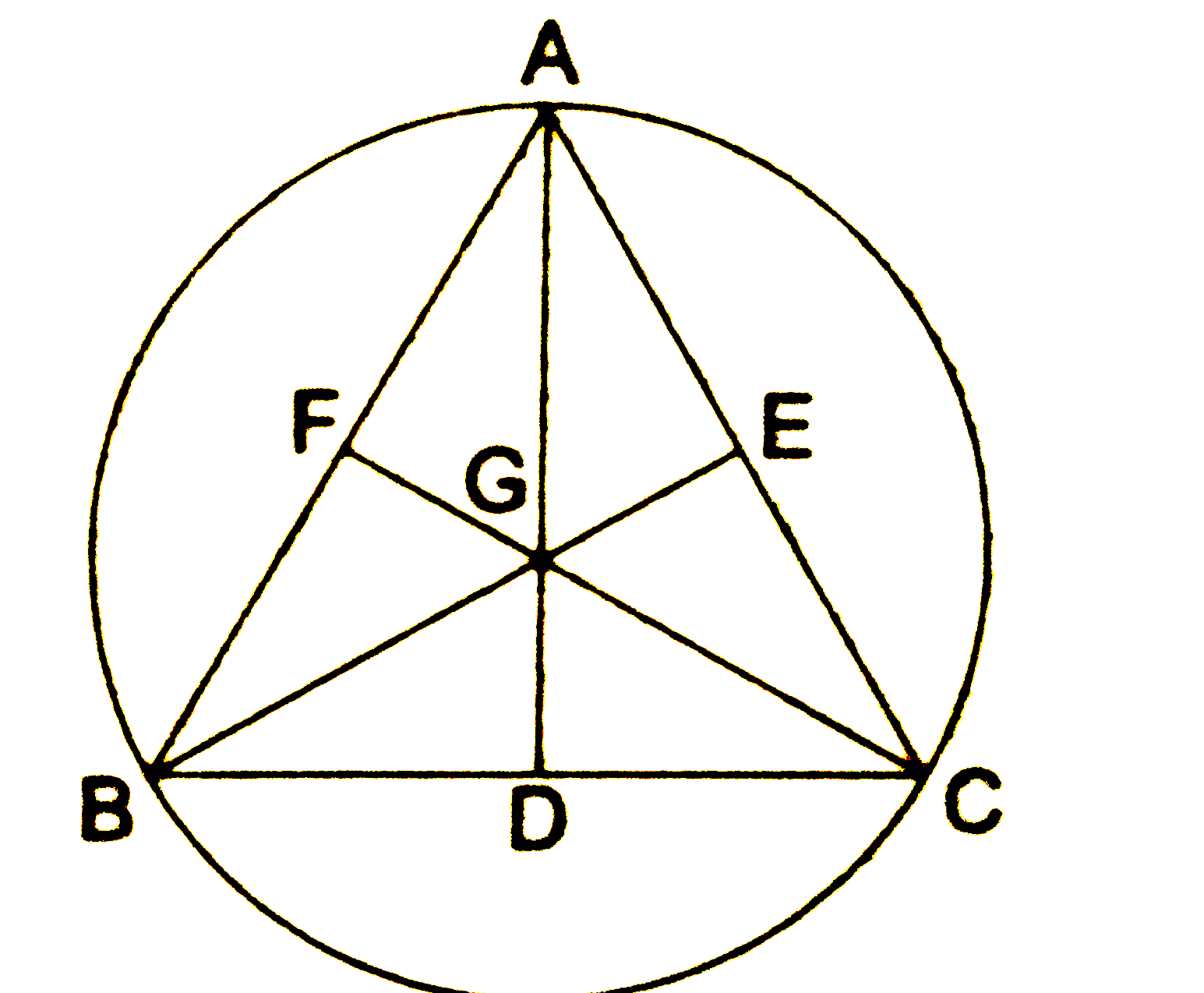
- In an equilateral triangle prove that the centroid and the centre of t...
Text Solution
|
- In an equilateral triangle prove that the centroid and the centre of t...
Text Solution
|
- In an equilateral triangle, prove that the centroid and the circumcent...
Text Solution
|
- If the centroid of an equilateral triangle is (1,1) and its one vertex...
Text Solution
|
- किसी समबाहु त्रिभुज के परिवृत्त और अंत: वृत्त त्रिज्या में क्या अनुपात...
Text Solution
|
- CIRCUMCIRCLE AND CIRCUMCENTRE,ORTHOCENTRE AND CENTROID
Text Solution
|
- एक समबाहु त्रिभुज में, सिद्ध कीजिए कि केन्द्रक और परिवृत्त का केन्द्र ...
Text Solution
|
- In an equilateral triangle, the incentre, circumcentre, orthocentre an...
Text Solution
|
- In a triangle, if orthocentre, circumcentre, incentre and centroid coi...
Text Solution
|