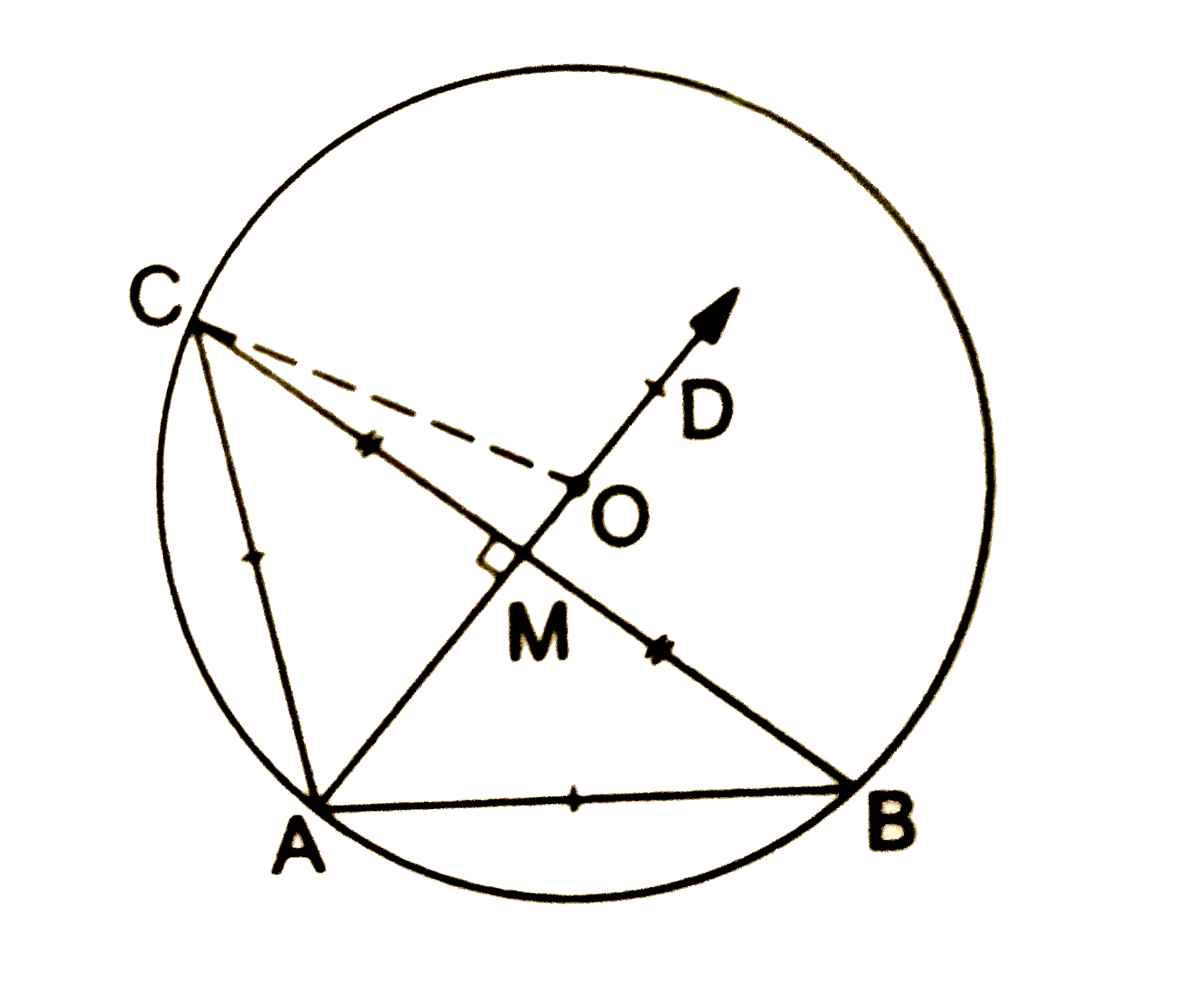
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- In a circle of radius 5\ c m ,\ A B\ a n d\ A C are two chords such t...
Text Solution
|
- In a circle of radius 5cm,AB and AC are two chords such that AB=AC=6cm...
Text Solution
|
- AB and CD are two chords of a circle such that AB = 6 cm, CD = 12 cm a...
Text Solution
|
- A B\ a n d\ C D are two chords of a circle such that A B=6\ c m ,\ C...
Text Solution
|
- A B C is a triangle with B as right angle, A C=5\ c m\ a n d\ A B=...
Text Solution
|
- A B\ a n d\ C D are two parallel chords of a circle with centre O su...
Text Solution
|
- A B and C D are two chords of a circle such that A B=6c m ,C D=12c m a...
Text Solution
|
- A B and C D are two parallel chords of a circle such that A B=10c m an...
Text Solution
|
- A B and C D are two parallel chords of a circle whose diameter is A C ...
Text Solution
|