Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
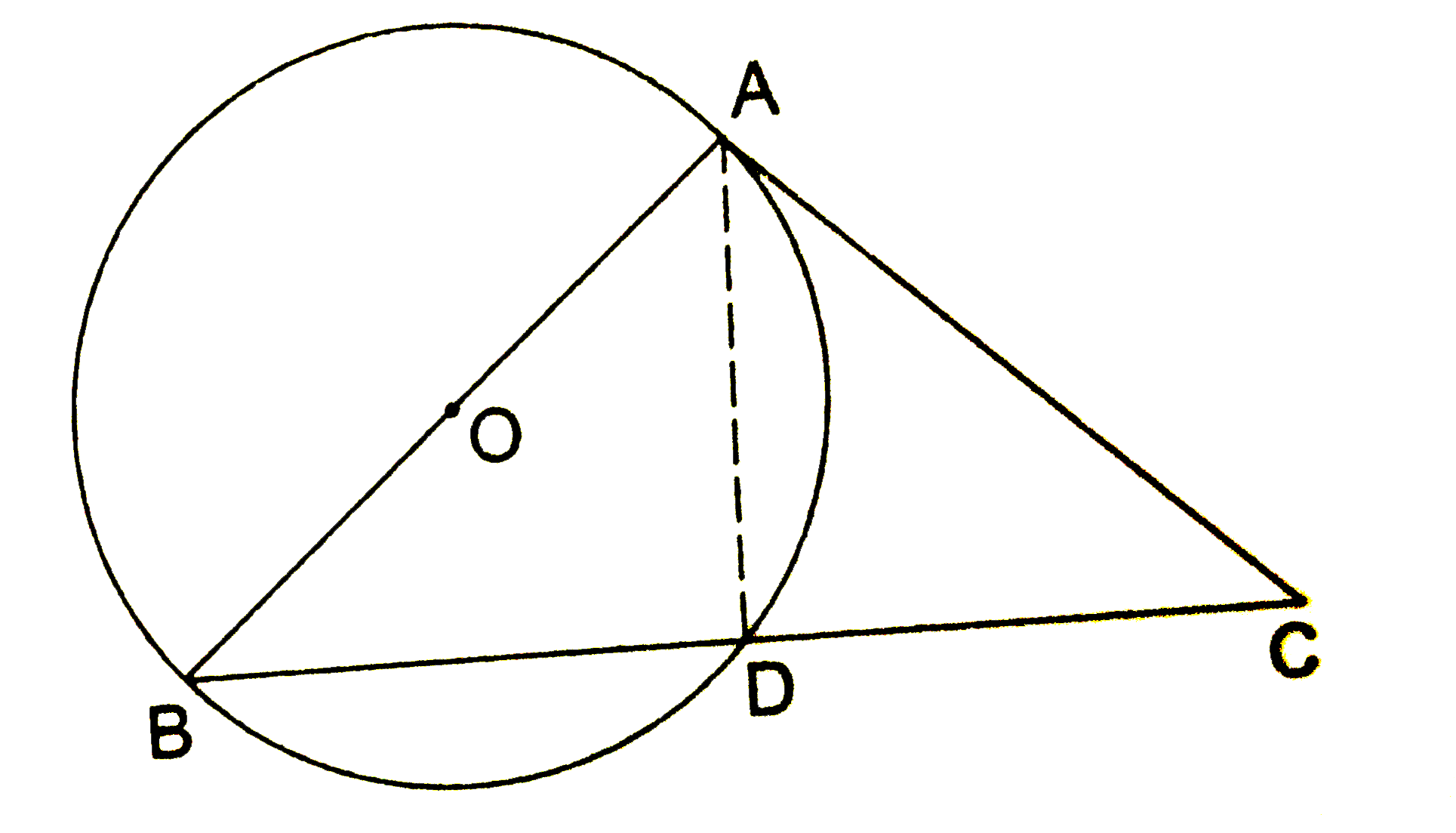
- Prove that the circle drawn on any one of the equal sides of an iso...
Text Solution
|
- Prove that the circle drawn on any one of the equal sides of an isos...
Text Solution
|
- Prove that the circle drawn on any one of the equal sides of an iso...
Text Solution
|
- Prove that the circle drawn on any one of the equal sides of an isosc...
Text Solution
|
- सिद्ध कीजिए कि किसी समद्विबाहु त्रिभुज कि बराबर भुजाओं में से किसी एक ...
Text Solution
|
- किसी समद्विबाहु त्रिभुज की बराबर भुजाओं में से एक को व्यास मानकर खींचा...
Text Solution
|
- Prove that the circle drawn with any one of the equal sides of an isos...
Text Solution
|
- सिध्द करो कि किसी समद्विबाहु त्रिभुज कि समान भुजाओ में से किसी भी एक भ...
Text Solution
|
- Prove that a circle drawn on any of the two equal sides of an isoscele...
Text Solution
|