Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
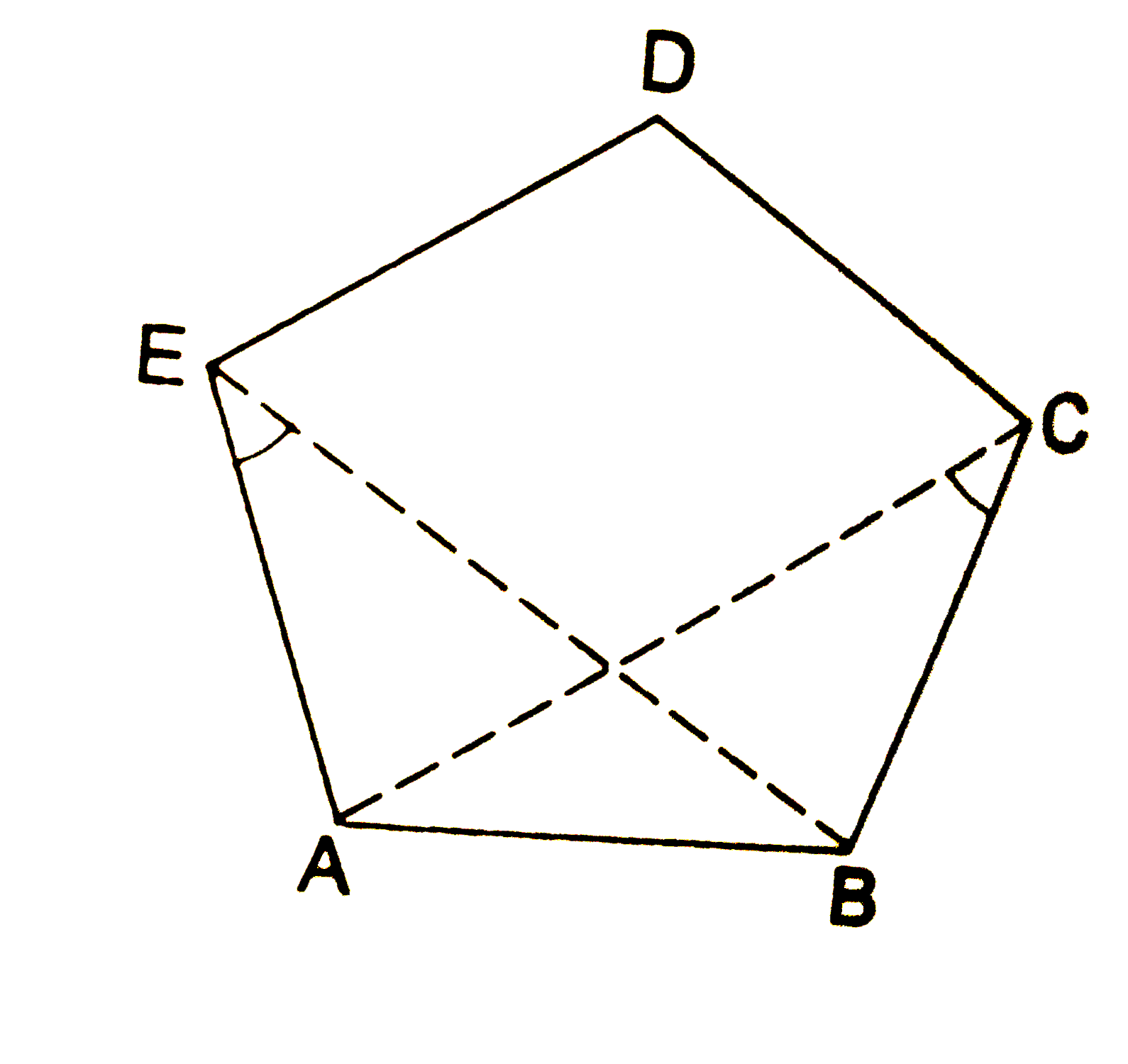
- Prove that any four vertices of a regular pentagon are concyclic.
Text Solution
|
- Symmetry of a regular pentagon.
Text Solution
|
- Lines of symmetry of a regular pentagon
Text Solution
|
- Area of regular polygon: regular hexagon and regular pentagon
Text Solution
|
- Four particles each having a charge q are placed on the four vertices ...
Text Solution
|
- Prove that any four vertices of a regular pentagon are concyclic.
Text Solution
|
- सिद्ध कीजिए कि एक समपंचभुज के कोई चार शीर्ष चक्रीय होते हैं |
Text Solution
|
- Prove that any four vertices of regular pentagon are concyclic .
Text Solution
|
- A regular pentagon has four charges each +q at four of its vertices. A...
Text Solution
|