Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
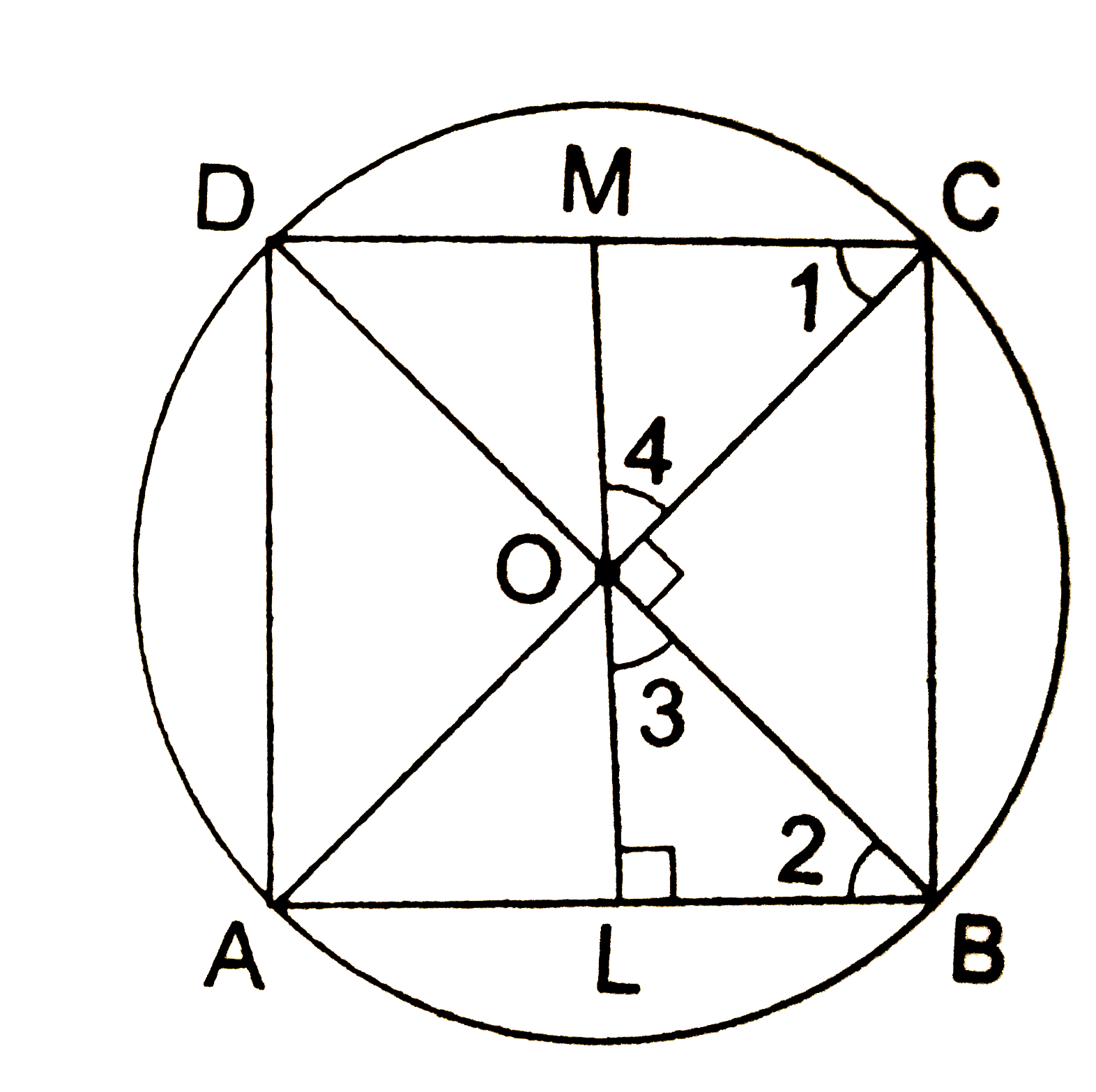
- The diagonals of a cyclic quadrilateral are at right angles. Prove tha...
Text Solution
|
- The bisectors of the angles formed by producing the opposite sides of ...
Text Solution
|
- The diagonals of a quadrilateral are of lengths 6cm and 8cm. If the di...
Text Solution
|
- If the exterior angle of a quadrilateral formed by producing one of it...
Text Solution
|
- Prove that the bisectors of the angles formed by producing the opposit...
Text Solution
|
- The diagonals of a cyclic quadrilateral are at right angles. Prove tha...
Text Solution
|
- यदि चक्रीय चतुभुर्ज के विकर्ण एक-दूसरे को वृत्त के केन्द्र पर समकोण पर...
Text Solution
|
- एक चतुर्भुज की चारों भुजाएँ बराबर है तो सिद्ध कीजिए कि इसके कोण ,...
Text Solution
|
- If the diagonals of a cyclic quadrilateral are perpendicular to each ...
Text Solution
|