Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
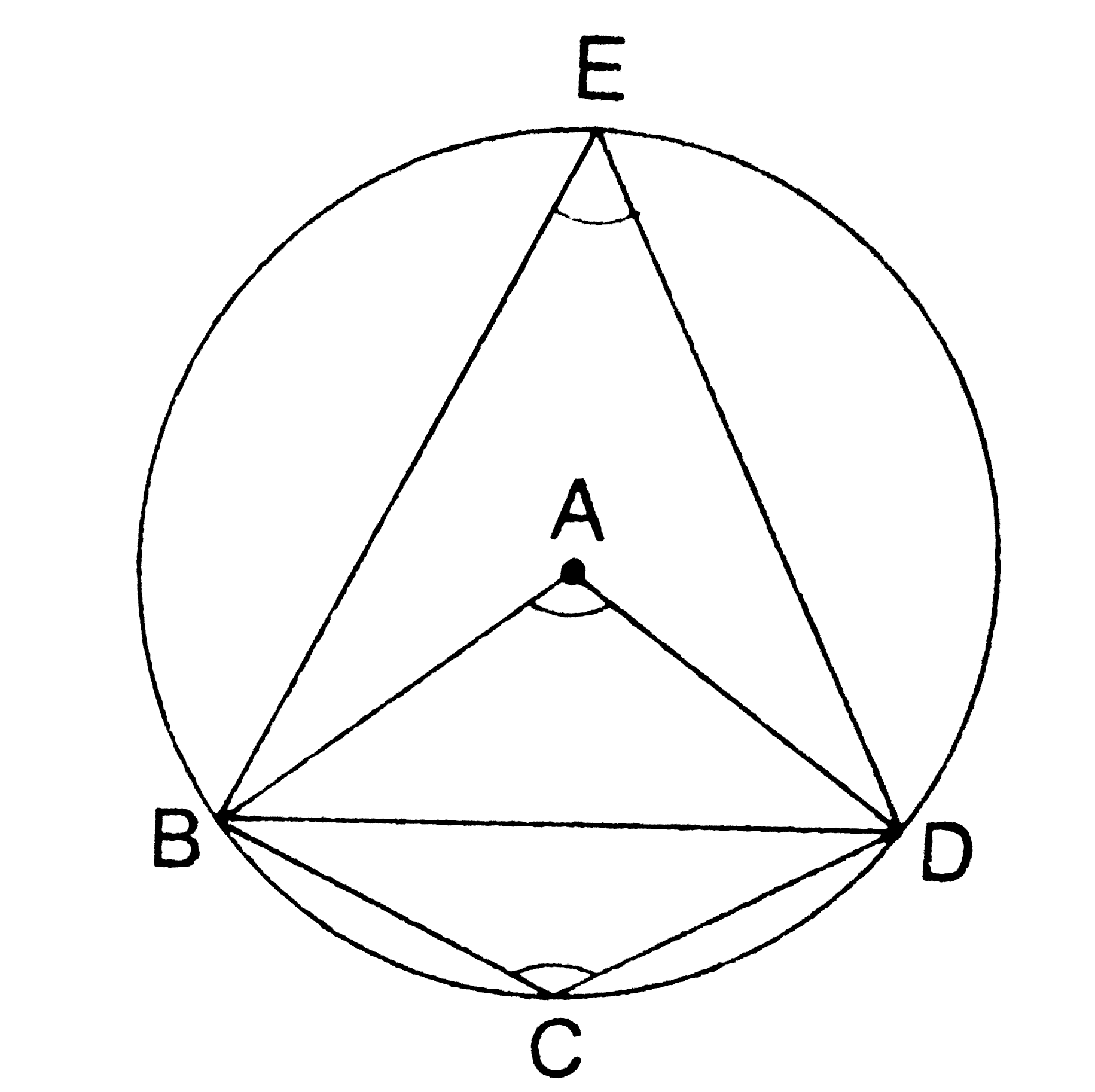
- ABCD is such a quadrilateral that A is the centre of the circle passin...
Text Solution
|
- A circle passes through A,B,C and D as shown in the figure.If /BAD=63,...
Text Solution
|
- ABCD is a quadrilateral in which /ABC=/BCD and CD>AB Prove that /BAD>/...
Text Solution
|
- ABCD is such a quadrilateral that A is the centre of the circle passin...
Text Solution
|
- Let ABCD be a quadrilateral with /CBD=2/ADB, /ABD=2/CDB, AB=BC, then
Text Solution
|
- Draw a circle with the point a of quadrilateral ABCD as centre which p...
Text Solution
|
- एक चतुर्भुज ABCD में AB = AC = AD हों, तो सिद्ध कीजिए कि /BAD = 2(/BDC...
Text Solution
|
- एक चतुर्भुज ABCD में AB=AC=AD हों तो सिद्ध कीजिए कि /BAD=2(/BDC+/CBD).
Text Solution
|
- A quadrilateral ABCD is drawn to circumscribe a circle. Prove that A ...
Text Solution
|