In `DeltaA B C`, D, E and F are respectively the mid-points of sides AB, BC and CA. Show that `DeltaA B C`is divided into four congruent triangles by joining D, E and F.

Explanation

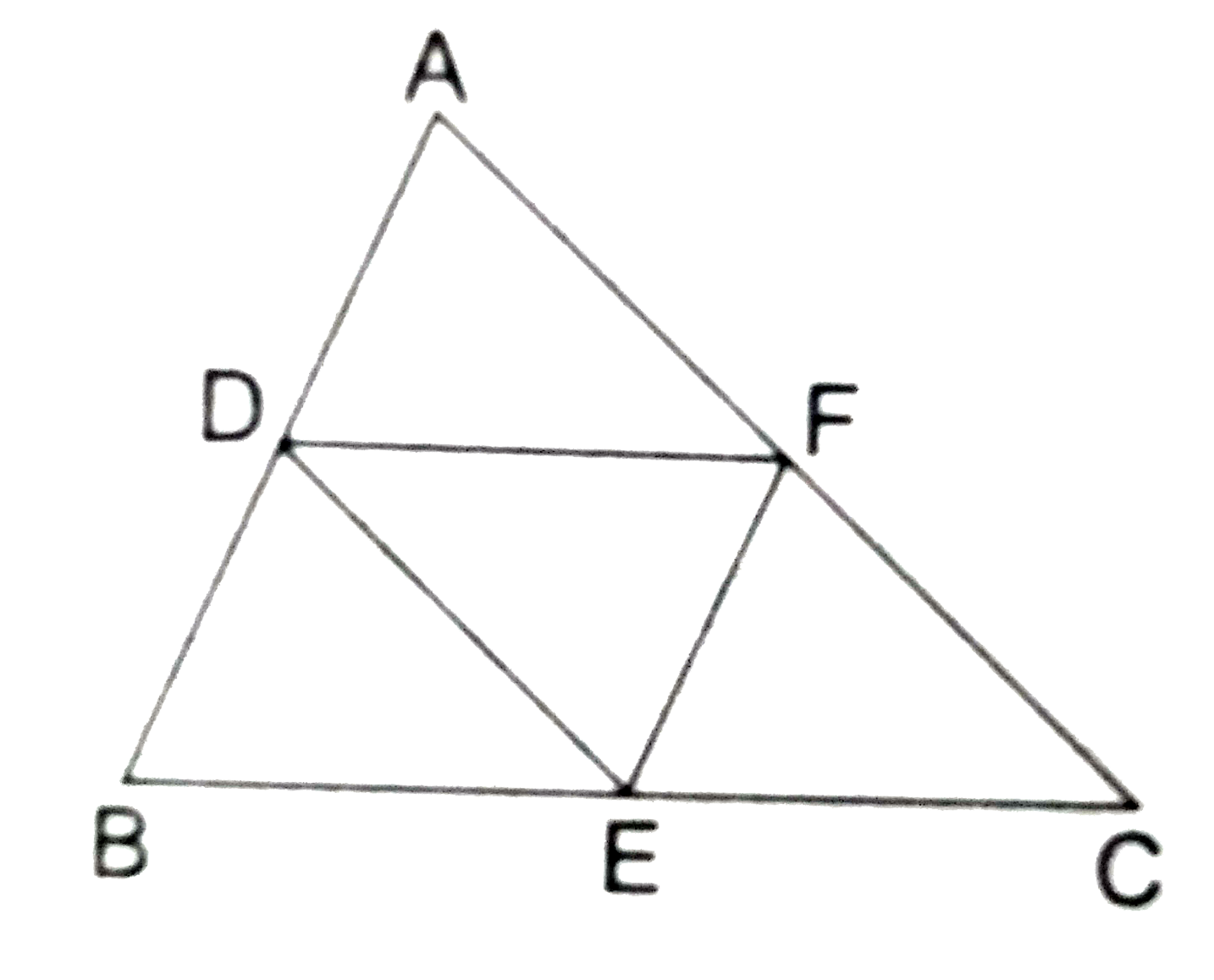
D and F are the midpoints of sides AB and AC respectively of `triangle ABC.`
`therefore ` DF||BC.
Similarly, DE||AC and EF||AB.
Now, DF||BE and EF||BD
`rArr DBEF ` is a ||gm
`rArr triangle EDB ~= triangle DEF " "[ because " De is a diagonal of ||gm DBEF"].`
[NOTE Any diagonal of a ||gm divides it into two congruent triangles.]
Similarly, `triangle CFE ~= triangle FAD ~= triangle DEF.`
Hence, all the four triangles are congruent.