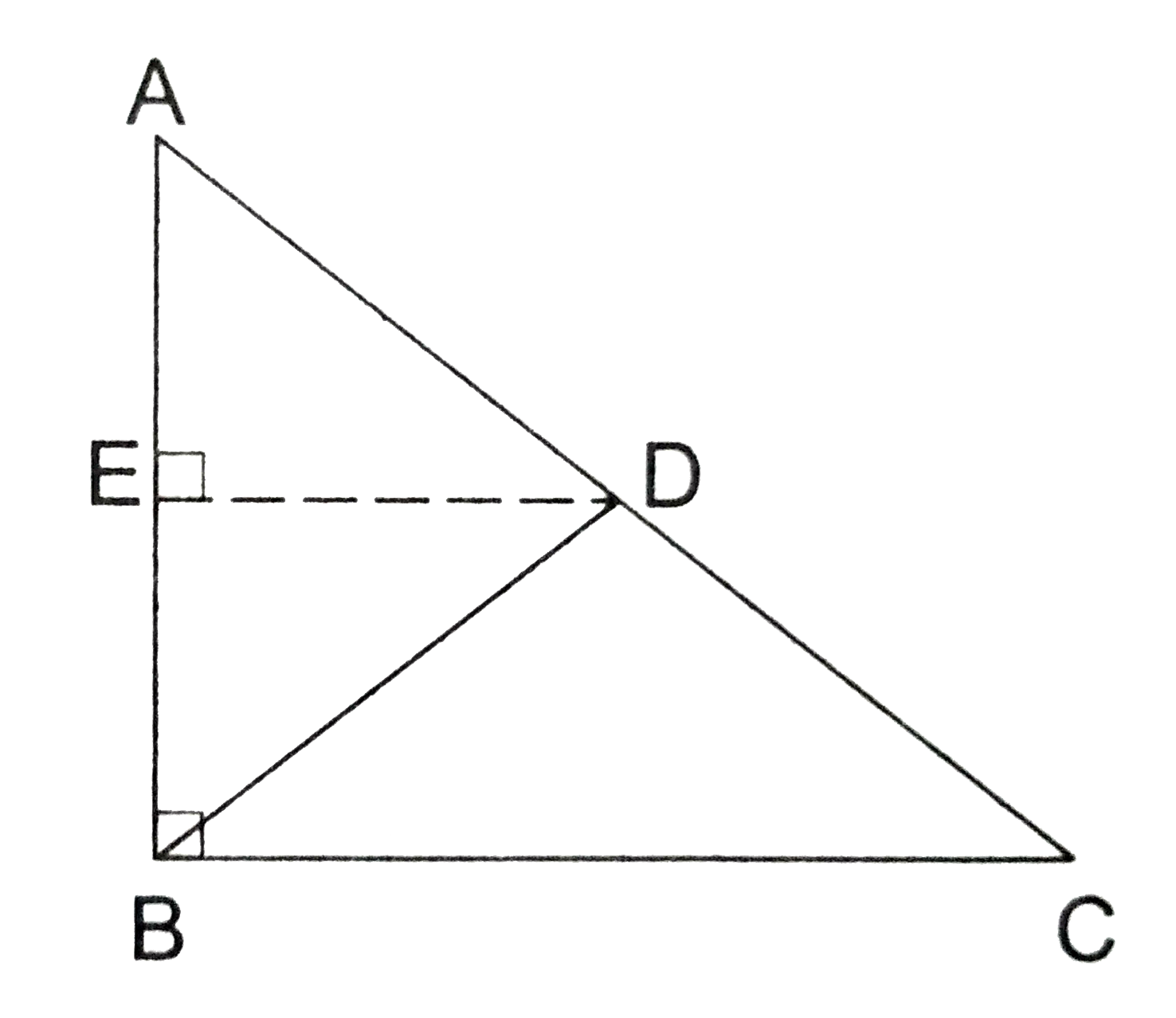
Through D, draw DE||BC, meeting AB at E.
Now, ` angle AED = angle ABC =90^(@) " " ["corres. " angle ]`
`therefore angle BED = angle AED = 90^(@) " [ because angle AED + angle BED = 180^(@)].`
Now, in `triangle ABC,` it is given that D is the midpoint of AC and DE||BC (by construction).
`therefore ` E must be the midpoint of AB (by converse of midpoint theorem).
`therefore AE = BE.`
Now, in `triangle ` AED and BED, we have
`AE=BE " (proved), " ED=ED " " ` (common),
`angle AED = angle BED " " ("each equal to "90^(@)).`
` therefore triangle AED ~= triangle BED `
`therefore DA = DB.`
But, `DA = DC " " [ because " D is the midpoint of AC"].`
Hence, `DA= DB=DC.`