The figure formed by joining the mid-points of the adjacent sides of a quadrilateral is

Explanation

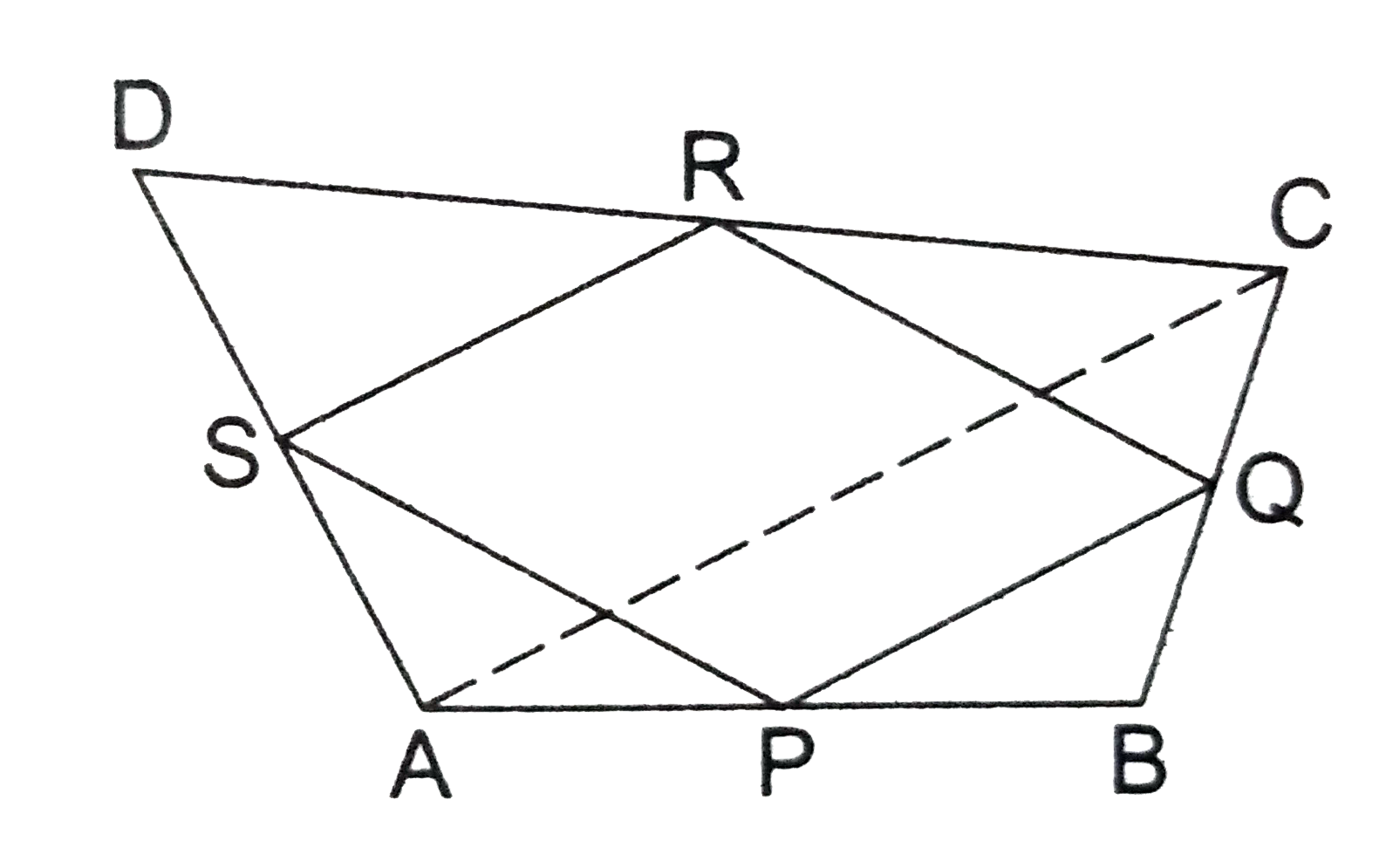
Let ABCD be a quadrilateral in which P, Q, R, S are the midpoints of AB, BC, CD and DA respectively. Join AC.
In `triangle `ABC, the points P and Q are the midpoints of AB and BC respectively.
`therefore " PQ ||AC and "PQ=(1)/(2) AC " " ` (by midpoint theorem).
Again , in `triangle ` DAC, the points S and R are the midpoints of AD and DC respectively.
`therefore " SR||AC and " SR=(1)/(2) AC " " ` (by midpoint theorem).
Now, PQ||AC and and SR||AC `rArr ` PQ||SR.
Also, `PQ=SR " " ("each equal to "(1)/(2)AC).`
`therefore " PQ||SR and " PQ=SR.`
Hence, PQRS is a parallelogram.