GIVEN A trapezium ABCD in which E and F are midpoints of sides AD and BC respectively .
TO PROVE (i) EF||AB, ` " (ii) " EF=(1)/(2) (AB+CD).`
CONTRUCTION Join DF and produce it to meet AB produced in P.
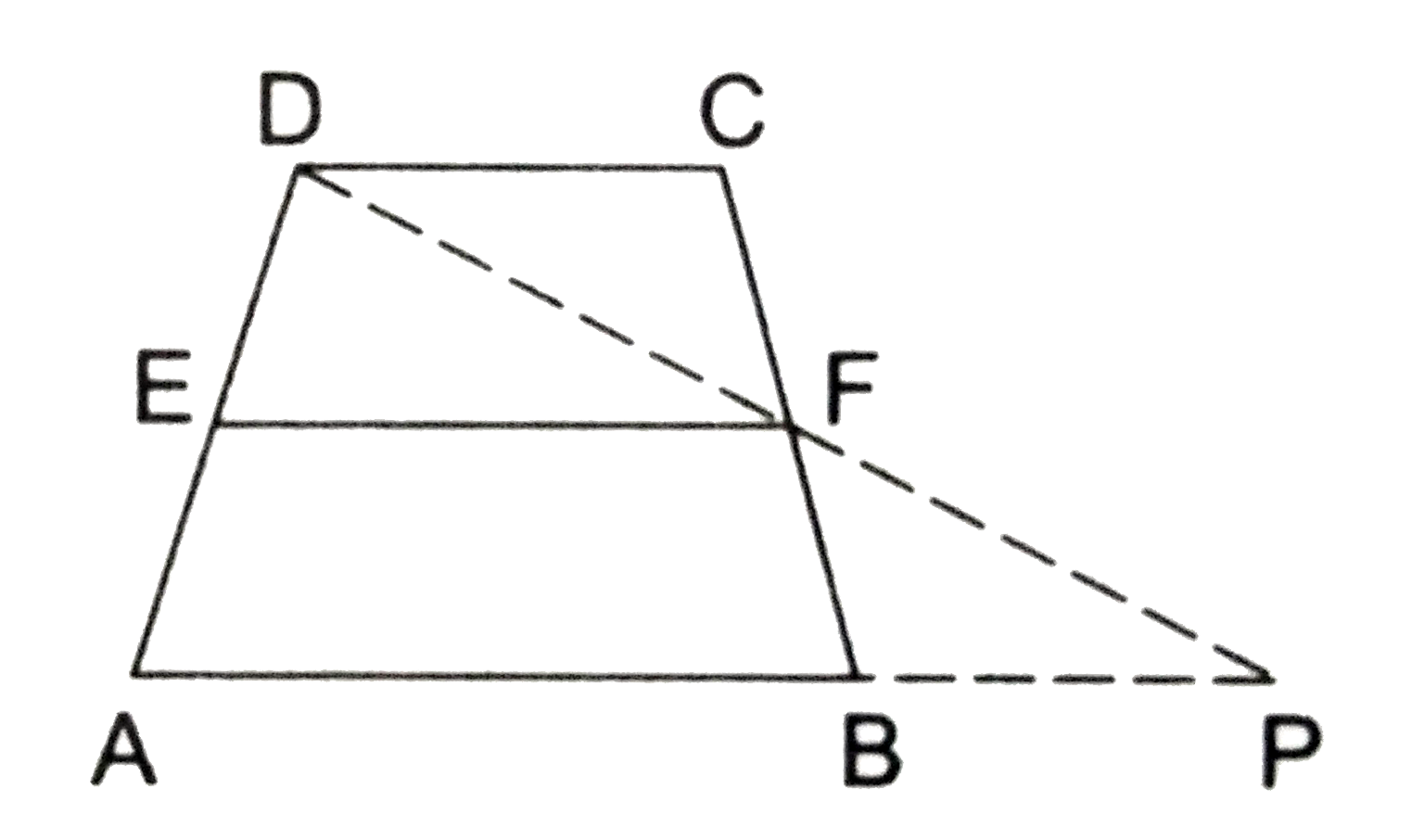
PROOF In `triangle`DCF and PBF we have
`angle DFC = angle PFB " " ( "vert . opposite " angle )`
`CF=BF " " (because " F is the midpoint of BC")`
`angle DCF = angle PBF " " ("alt. interior " angle )`
`therefore triangle DCF ~= triangle PBF " " ` (ASA-criterion).
And so, `DF=PF and CD = BP " " `(c.p.c.t.).
Now, in `triangle`DAP, we have
E is the midpoint of AD and F is the midpoint of DP. ` " " [ because DF=PF]`
`therefore " EF||AP and " EF=(1)/(2)AP " " `[by midpoint theorem]
`rArr " EF||AB and " EF =(1)/(2) (AB+BP).`
Hence, EF||AB and `EF=(1)/(2)(AB+CD).`