Prove that the line joining the mid-points of the diagonals of a trapezium is parallel to the parallel sides of trapezium and is half of their difference.

Explanation

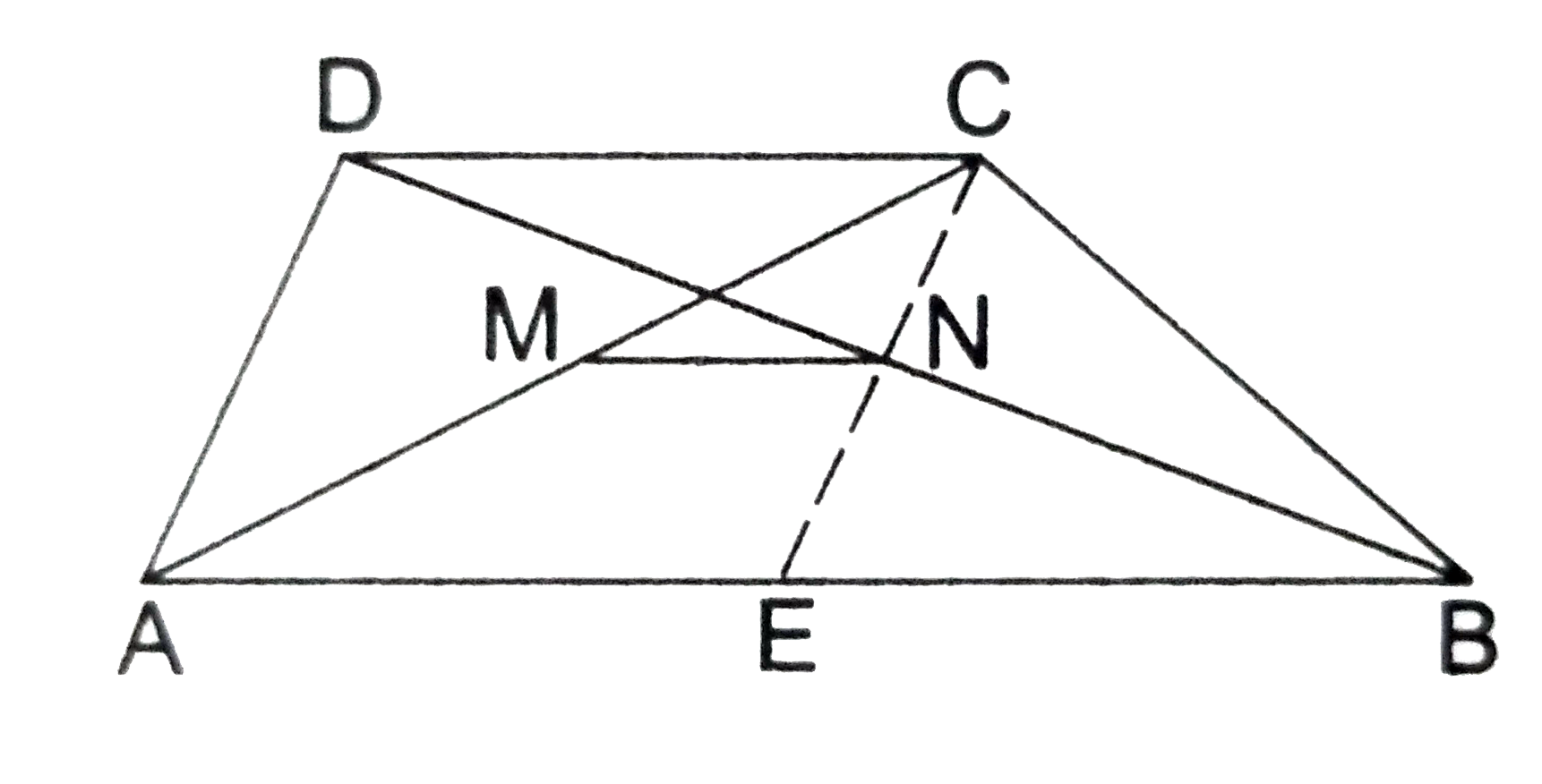
Let ABCD be a trapezium in which AB||DC, and let M and N be the midpoints of the diagonals AC and BD respectively.
Join CN and produce it to meet AB at E.
In `triangle` CDN and EBN, we have:
`DN=BN " " [ because " N is midpoint of BD"]`
`angle DCN = angle BEN " " ("alt,interior "angle)`
`angle CDN = angle EBN " " ("alt. interior " angle )`
`therefore triangle CDN ~= triangle EBN " " `[SAA-criterial].
`therefore DC = EB and CN=NE " " `(c.p.c.t.).
Thus, in `triangle`CAE, the points M and N are the midpoints of AC and CE respectively.
`therefore "MN||AE and "MN=(1)/(2) AE rArr` MN||AB||DC
`and MN=(1)/(2) AE=(1)/(2)(AB-EB)=(1)/(2) (AB-DC) " " [ because EB=DC].`