ABCD is a trapezium in which `A B\ ||\ D C`, BD is a diagonal and E is the mid-point of AD. A line is drawn through E parallel to AB intersecting BC at F (see Fig. 8.30). Show that F is the mid-point of BC.

Explanation

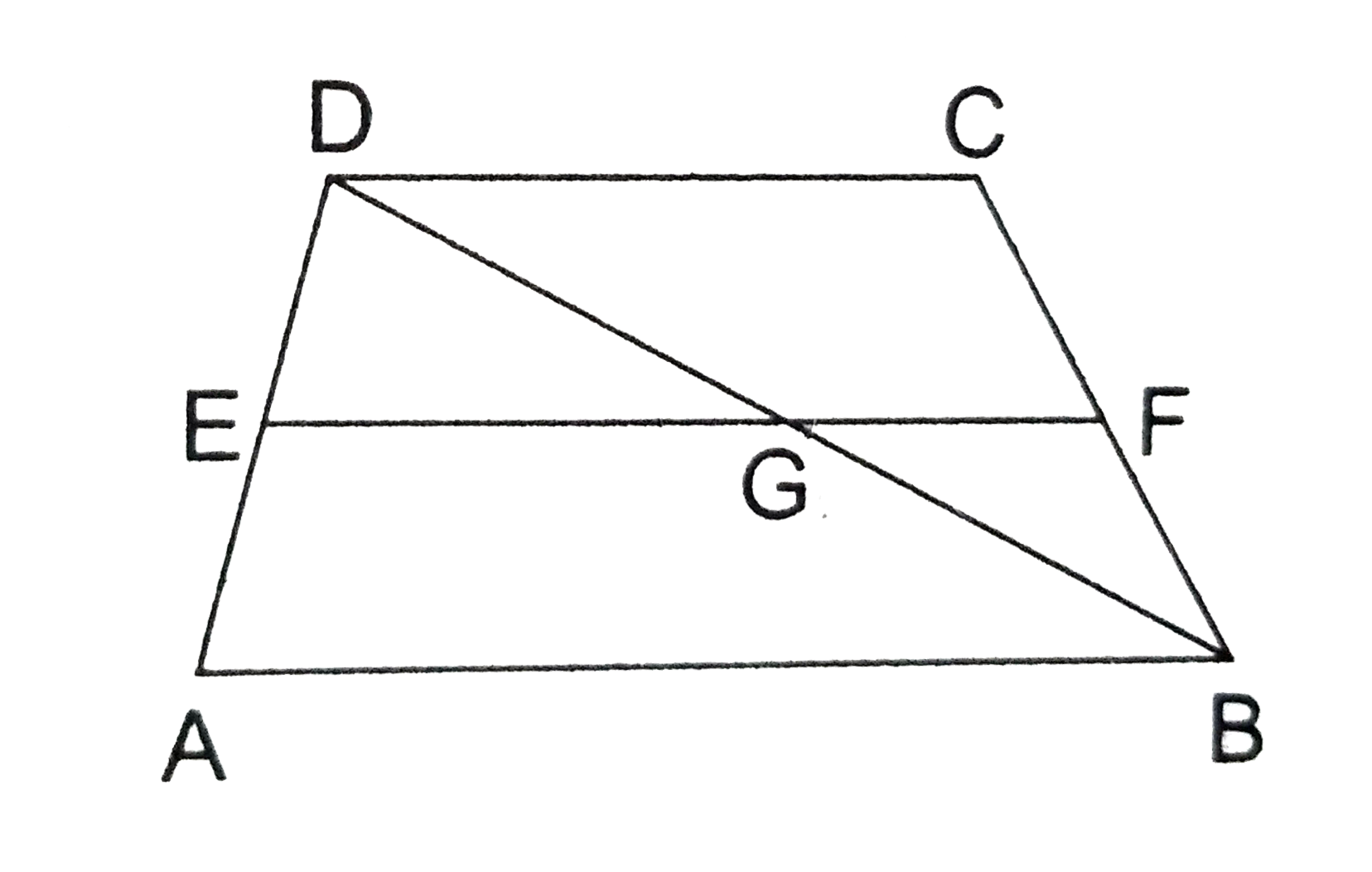
GIVEN A trapezium ABCD in which AB||DC. E is the midpoint fo side AD. A line EF is drawn parallel to AB intersecting BC at F.
TO PROVE F is the midpoint of BC.
CONSTRUCTION Join BD. Let BD intersect EF at G.
PROOF In `triangle`DAB, we have
E is the midpoint of AD and EG||AB.
`therefore ` G is the midpoint of BD [ by converse of midpoint theorem].
Now, in `triangle BCD`, we have
G is the midpoint of BD and GF||DC
` " " [because" EF||AB and AB||DC " rArr "EF ||DC"].`
Hence, F is the midpoint of BC [by converse of midpoint theorem].