Home
Class 9
MATHS
ABC is a triangle right-angled at C. A l...

ABC is a triangle right-angled at C. A line through the midpoint P of hypotenuse AB and parallel to BC intersects AC at M. Show that
`"(i) "` M is the midpoint of `AC,`
` "(ii) " MP bot AC ,`
` "(iii) " CP = AP=(1)/(2)AB. `

Text Solution

Verified by Experts


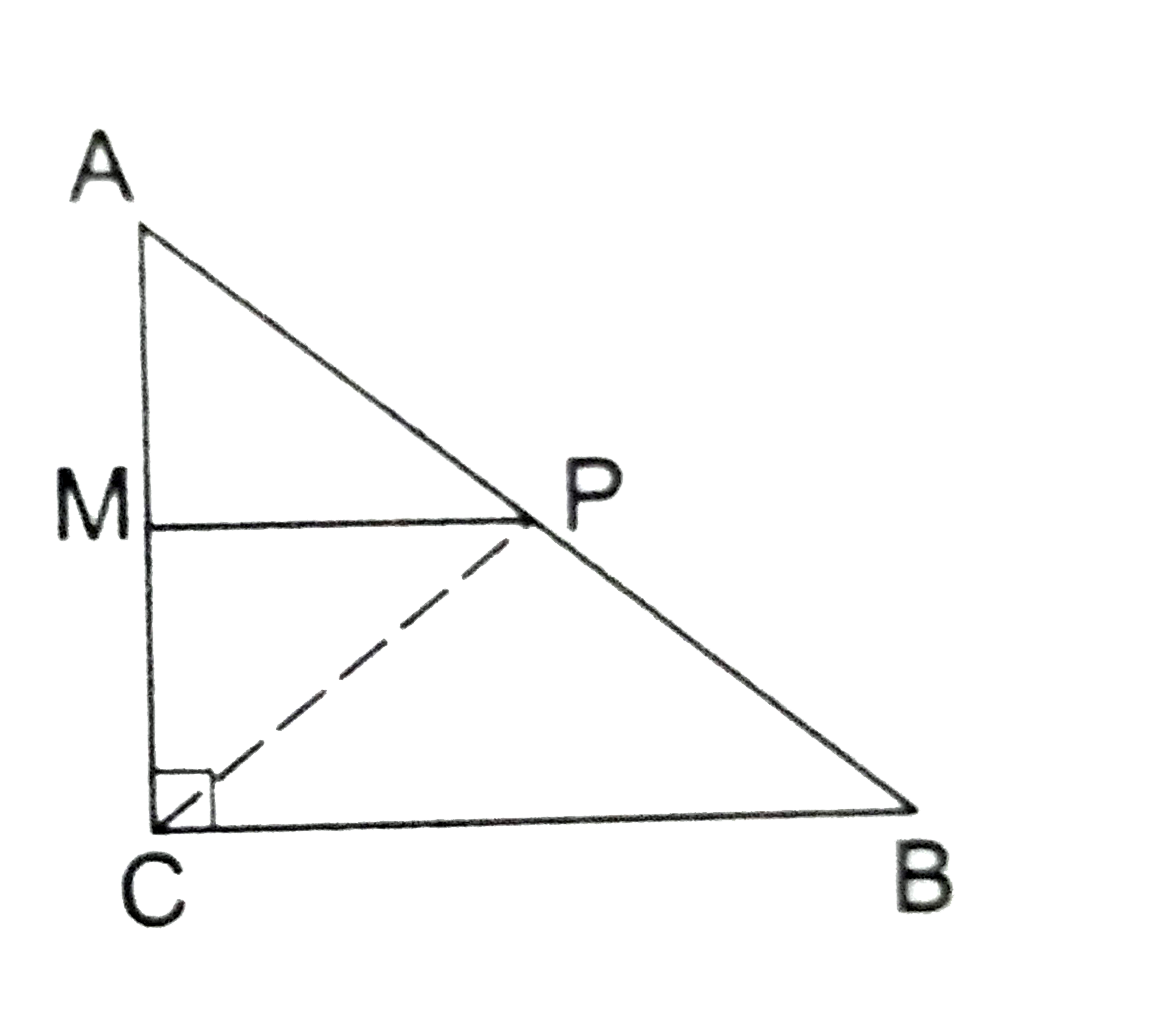
In `triangle ACB`, we have
P is the midpoint of AB and PM||BC.
`therefore ` M is the midpoint of AC.
[by converse of midpoint theorem].
Now, PM||BC.
`therefore angle PMC + angle BCM=180^(@) " " ("co-interior "angle )`
`rArr angle PMC + 90^(@) =180^(@) rArr angle PMC=90^(@).`
Thus, `MP bot AC.`
Join PC.
In `triangle PMA` and PMC, we have:
`MA= MC " " [because " M is the midpoint of AC"]`
`angle PMA = angle PMC " " ("each equal to "90^(@))`
`PM=PM " " `(common)
`therefore triangle PMA ~=triangle PMC " " `(SAS-criterion).
And so, `AP=CP " " `(c.p.c.t.).
Now, P is the midpoint of AB.
`therefore CP=AP=(1)/(2)AB.`
Promotional Banner

Topper's Solved these Questions

  • QUADRILATERALS

    RS AGGARWAL|Exercise EXAMPLE|32 Videos

  • QUADRILATERALS

    RS AGGARWAL|Exercise Exercise 10 A|10 Videos

  • PROBABILITY

    RS AGGARWAL|Exercise Multiple Choice Questions (Mcq)|16 Videos

  • TRIANGLES

    RS AGGARWAL|Exercise MULTIPLE-CHOICE QUESTIONS (MCQ)|10 Videos

Similar Questions

Explore conceptually related problems

ABC is a triangle right angled at C. A line through the mid-point M of hypotenuse AB and parallel to BC intersects AC at D. Show that (i) D is the mid-point of AC (ii) M D_|_A C (iii) C M" "=" "M A=1/2A B

Let ABC be a triangle, right-angled at B and D be the midpoint of AC. Show that DA = DB = DC.

ABC is a triangle right angled at C. If AB=25cm and AC=7cm, find BC.

Delta ABC is a right triangle right angled at A such that AB=AC and bisector of /_C intersects the side AB at D.Prove that AC+AD=BC .

ABC is an isosceles triangle with AB = AC. A circle through B touching AC at the middle point intersects AB at P. Then, AP : AB is

ABC is an isosceles triangle with AB = AC. A circle through B touching AC at the middle point intersects AB at P. Then AP : AB is :

In Delta ABC, AB = AC. A circle is drawn with diameter AB and it intersects BC at D. Prove that D is the midpoint of BC.

ABC is right angle triangle where AD is perpendicular on hypotenuse BC. If AC = 2 AB find BD.

15m,BC=82.ABC is a triangle,right- angled at B. If AB=15m,BC=8m, find AC.