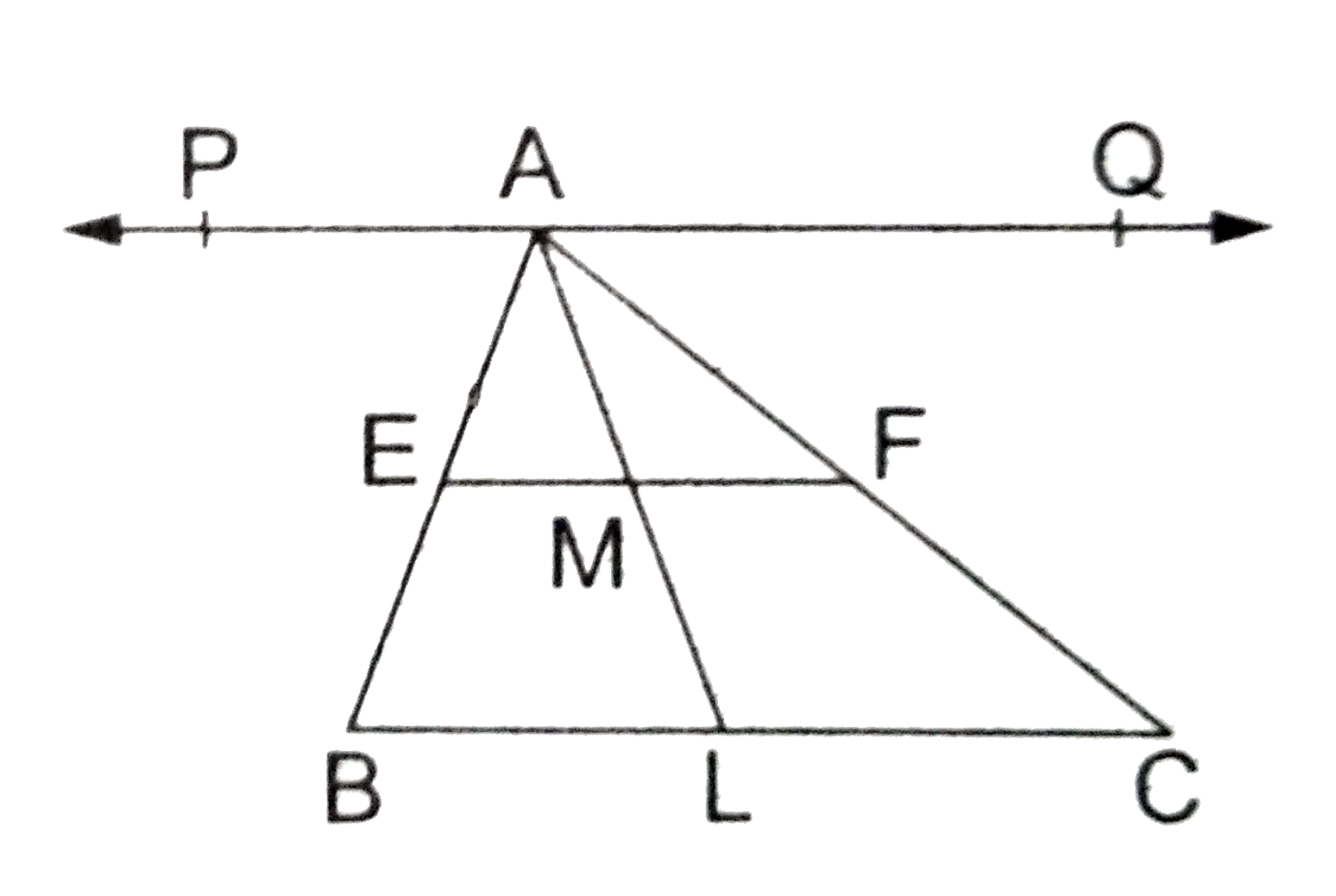
Text Solution
Verified by Experts
Topper's Solved these Questions
QUADRILATERALS
RS AGGARWAL|Exercise Exercise 10 A|10 VideosQUADRILATERALS
RS AGGARWAL|Exercise EXERCISE 10B|27 VideosQUADRILATERALS
RS AGGARWAL|Exercise Matching of Columns:|2 VideosPROBABILITY
RS AGGARWAL|Exercise Multiple Choice Questions (Mcq)|16 VideosTRIANGLES
RS AGGARWAL|Exercise MULTIPLE-CHOICE QUESTIONS (MCQ)|10 Videos
Similar Questions
Explore conceptually related problems
RS AGGARWAL-QUADRILATERALS-EXAMPLE
- If a diagonal of a parallelogram bisects one of the angles of the para...
Text Solution
|
- Let triangle ABC and triangle DEF be two triangles given in such a way...
Text Solution
|
- In the adjoining figure, ABCD is a parallelogram in which X and Y are ...
Text Solution
|
- In the adjoining figure, ABCD is a parallelogram and E is the midpoint...
Text Solution
|
- In the adjoining figure, AB = AC: CP||BA and AP is the bisector of ang...
Text Solution
|
- In the adjoining figure, ABCD is a parallelogram and the bisector of...
Text Solution
|
- In the adjoining figure, ABCD is a parallelogram, E is midpoint of AB ...
Text Solution
|
- ABCD is a trapezium in which AB||CD and AD = BC. Show that (i) angl...
Text Solution
|
- ABCD is a parallelogram in which E and F are the midpoints of the side...
Text Solution
|
- Let ABCD be a trapezium in which AB||DC and let E be the midpoint of A...
Text Solution
|
- In the adjoining figure, ABCD is a ||gm in which P is the midpoint of...
Text Solution
|
- In the adjoining figure, AD is a median of triangle ABC and E is the m...
Text Solution
|
- In the adjoining figure, ABCD is a trapezium in which AB||DC and AD = ...
Text Solution
|
- In the adjoining figure, ABCD and PQRC are rectangles, where Q is the ...
Text Solution
|
- In the given figure, D, E and F are the midpoints of the sides BC, CA ...
Text Solution
|
- In the adjoining figure, two points A and B lie on the same side of a ...
Text Solution
|
- In the adjoining figure, points M and N divide the side AB of triangl...
Text Solution
|
- E and F are respectively the midpoints of nonparallel sides AD and BC ...
Text Solution
|
- Prove that any line segment drawn from the vertex of a triangle to the...
Text Solution
|
- In the adjoining figure, the side AC of triangleABC is produced to E s...
Text Solution
|