Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
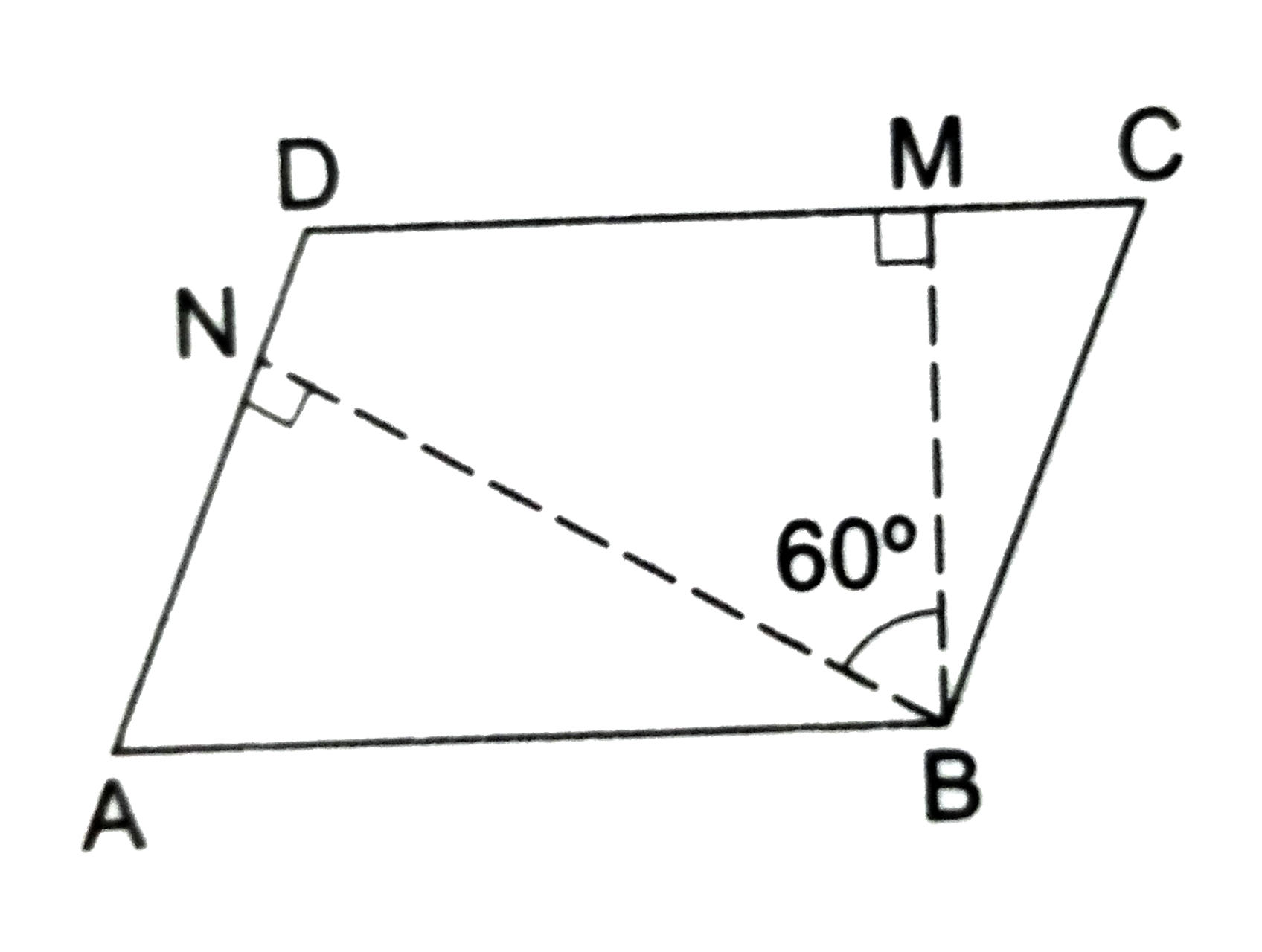
- The angle between the altitudes of a parallelogram, through the sam...
Text Solution
|
- If an angle of a parallelogram is two-third of its adjacent angle, fin...
Text Solution
|
- The angle between the altitudes of a parallelogram, through the sam...
Text Solution
|
- The angle between two altitudes of a parallelogram through the vertex ...
Text Solution
|
- If an angle of a parallelogram is four fifths of its adjacent angle, f...
Text Solution
|
- एक समान्तर चतुर्भुर्ज के एक अधिक कोण के शीर्ष से, समान्तर की दो ऊंचाइय...
Text Solution
|
- The angle between two altitudes of a parallelogram through the vertex ...
Text Solution
|
- If an angle of a parallelogram is two-third of its adjacent angle, ...
Text Solution
|
- If an angle of a parallelogram is two-third of its adjacent angle, f...
Text Solution
|