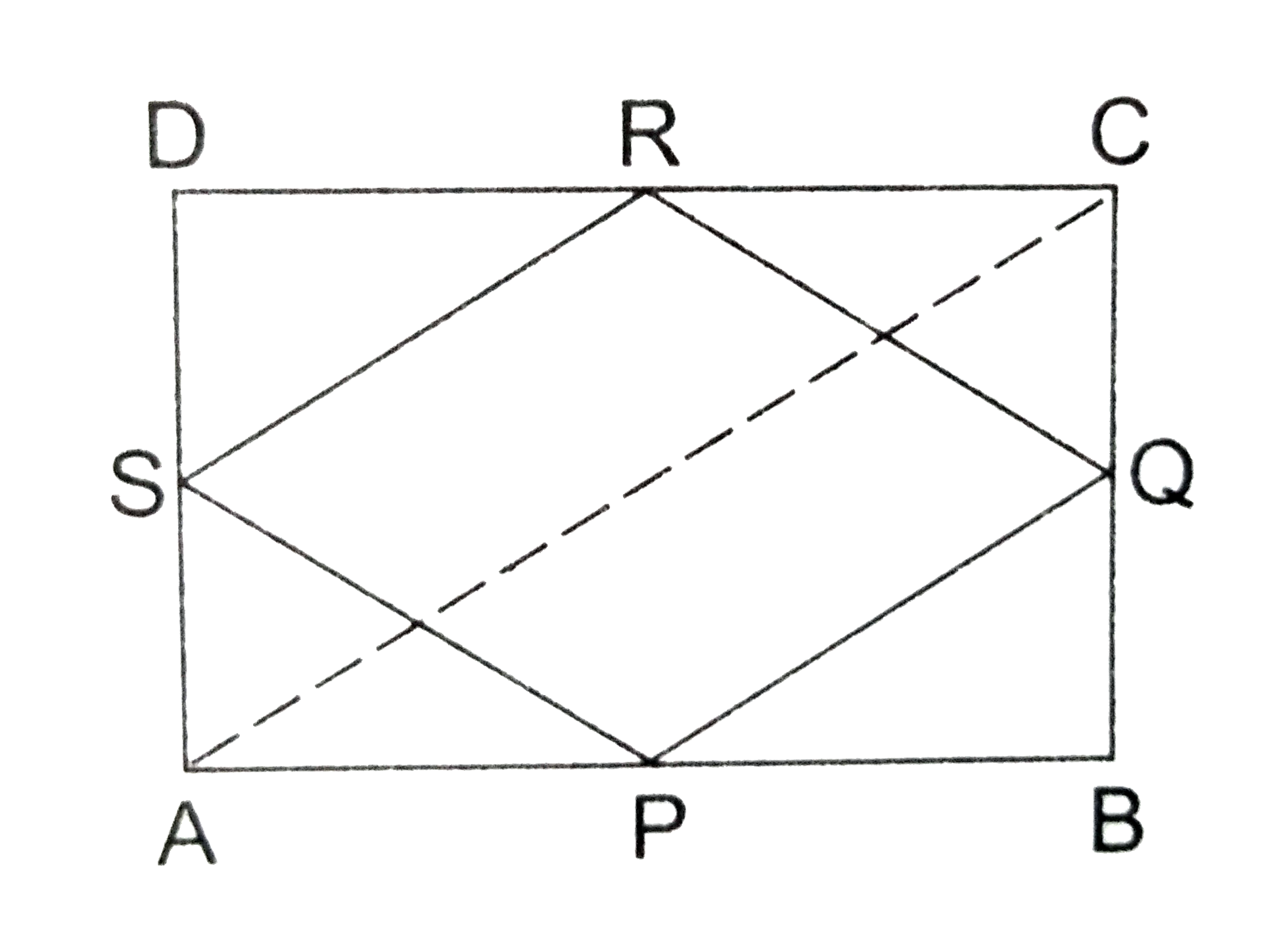
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- Show that the quadrilateral formed by joining the mid-points of the ...
Text Solution
|
- Show that the quadrilateral formed by joining the mid-points of the ...
Text Solution
|
- The figure formed by joining the mid-points of the adjacent sides o...
Text Solution
|
- The figure formed by joining the mid-points of the adjacent sides o...
Text Solution
|
- Show that the quadrilateral formed by joining the mid-points of the co...
Text Solution
|
- Show that the quadrialteral formed by joining the mid-points of the co...
Text Solution
|
- सिद्ध कीजिए कि एक आयत की क्रमागत भुजाओं के मध्य बिंदुओं को मिलाने से प...
Text Solution
|
- सिद्ध कीजिए की किसी आयत की क्रमिक भुजाओं के युग्मों के मध्य बिंदुओं क...
Text Solution
|
- Prove that the quadrilateral formed by joining the mid-points of the s...
Text Solution
|