Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
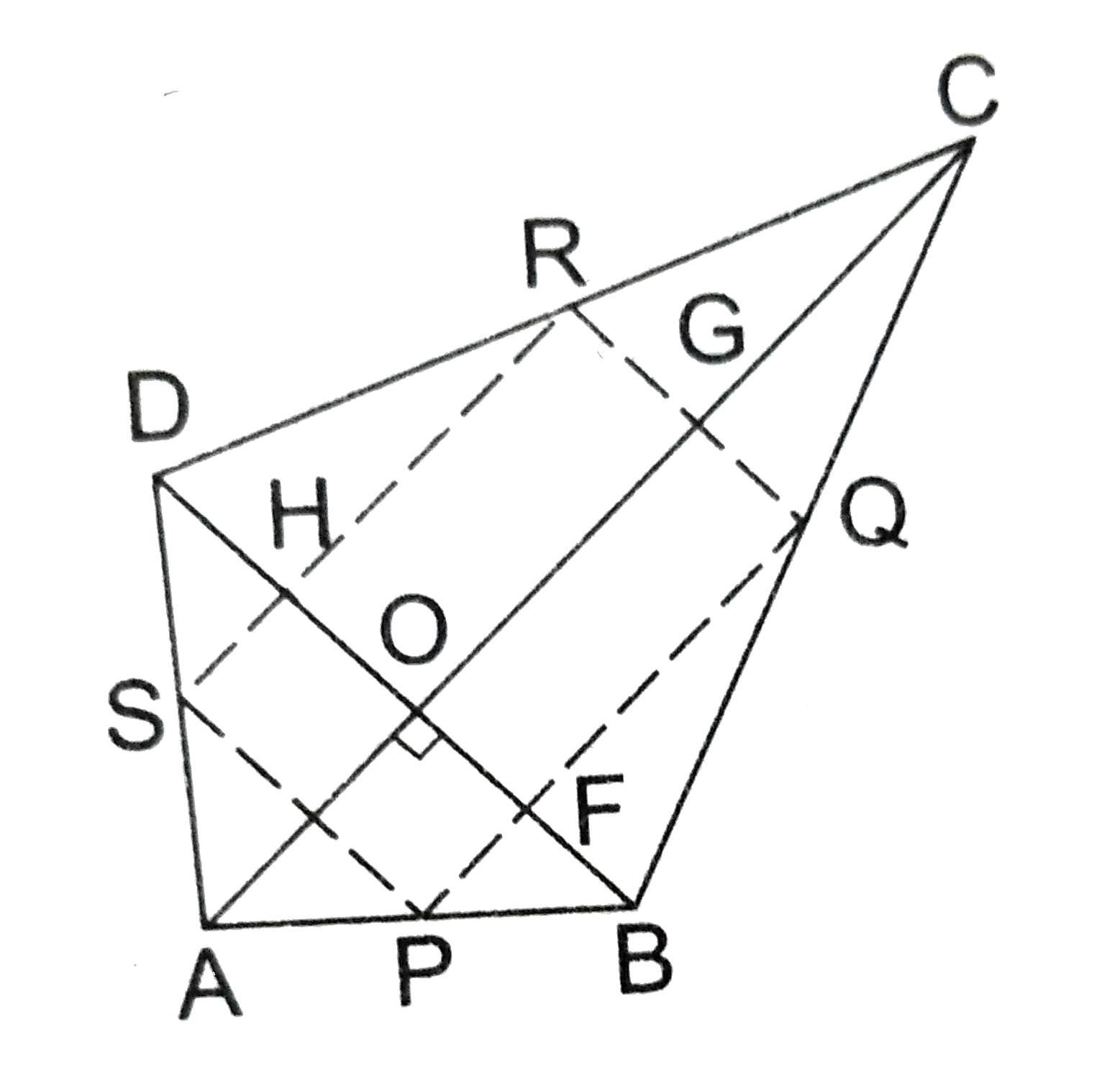
- The diagonals of a quadrilateral A B C D are perpendicular. Show that ...
Text Solution
|
- The diagonals of a quadrilateral A B C D are perpendicular. Show that ...
Text Solution
|
- Show that the quadrilateral formed by joining the mid-points of the ...
Text Solution
|
- The figure formed by joining the mid-points of the adjacent sides o...
Text Solution
|
- The figure formed by joining the mid-points of the adjacent sides o...
Text Solution
|
- The quadrilateral formed by joining the mid-points of the sides of a q...
Text Solution
|
- The diagonals of a quadrilateral ABCD are mutually perpendicular . Pro...
Text Solution
|
- Show that the quadrilateral formed by joining the mid-points of the co...
Text Solution
|
- Prove that the quadrilateral formed by joining the mid-points of the s...
Text Solution
|