Home
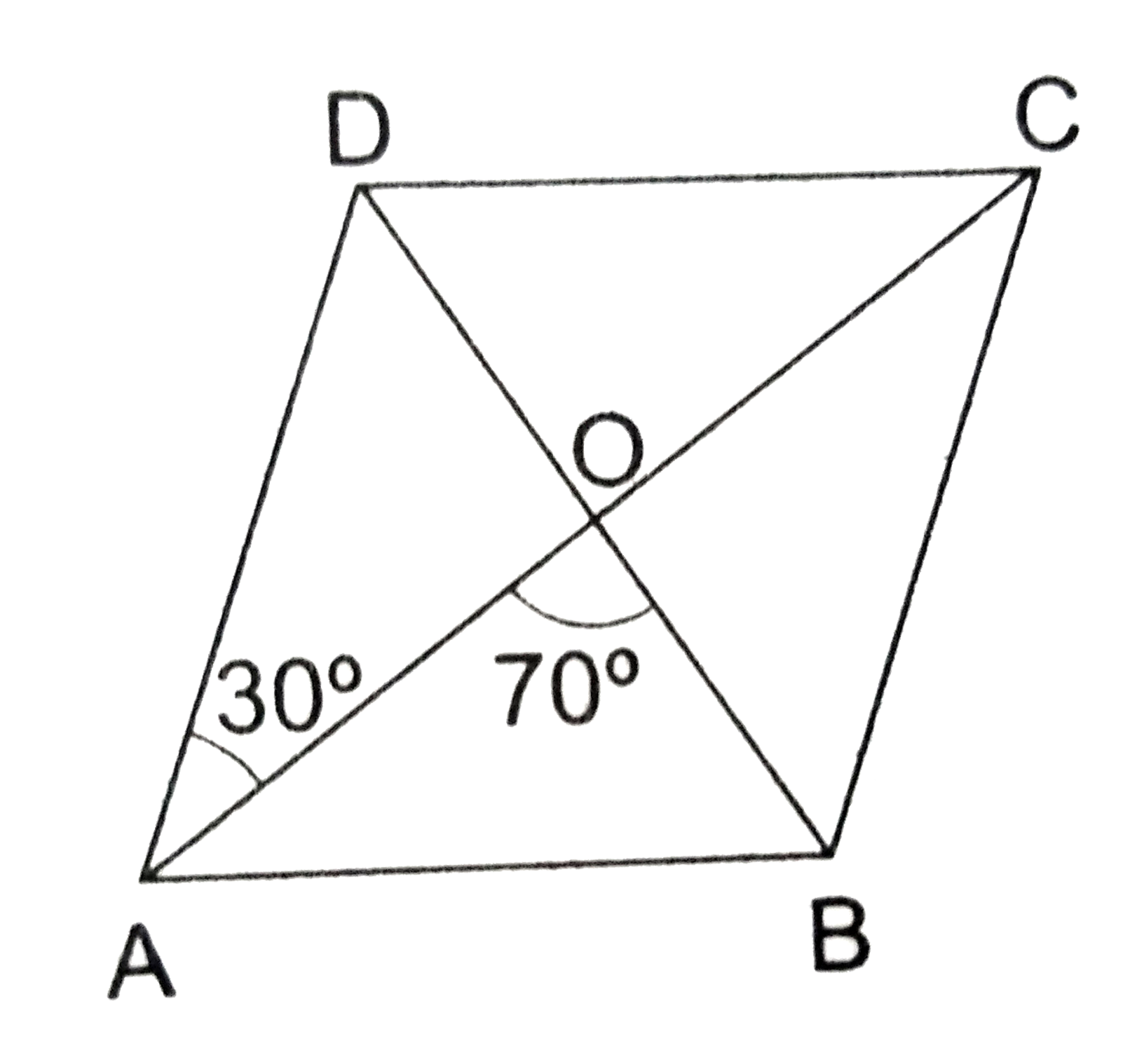
Class 9
MATHS
The diagonals AC and BD of a parallelogr...

The diagonals AC and BD of a parallelogram ABCD intersect each other at the point O such that `angle DAC =30^(@) and angle AOB=70^(@), " Then, " angle DBC=`?

A

`40^(@)`

B

`35^(@)`

C

`45^(@)`

D

`50^(@)`

Text Solution

Verified by Experts

The correct Answer is:
D
`angle AOC = angle DAC =30^(@) " "("alt. interior "angle )`
`rArr angle OCB =30^(@)`.
`angle AOB+angle BOC=180^(@) rArr 70^(@) + angle BOC =180^(@) rArr angle BOC=110^(@).`
In `triangle OBC, angle BOC +angle OCB + angle OBC =180^(@)`
`rArr 110^(@)+30^(@)+angle OBC =180^(@) rArr angle OBC =40^(@).`
Promotional Banner

Topper's Solved these Questions

  • QUADRILATERALS

    RS AGGARWAL|Exercise Short-Answer Questions|1 Videos

  • QUADRILATERALS

    RS AGGARWAL|Exercise Assertion - and - Reason Type MCQ|4 Videos

  • QUADRILATERALS

    RS AGGARWAL|Exercise Multiple Choice Questions (Mcq)|47 Videos

  • PROBABILITY

    RS AGGARWAL|Exercise Multiple Choice Questions (Mcq)|16 Videos

  • TRIANGLES

    RS AGGARWAL|Exercise MULTIPLE-CHOICE QUESTIONS (MCQ)|10 Videos

Similar Questions

Explore conceptually related problems

The diagonals AC and BD of a parallelogram ABCD intersect each other at the point O. If angle DAC = 32^(@) and angle AOB =70^(@), " find " angle DBC.

The diagonals AC and BD of a parallelogram ABCD intersect each other at the point O. If angleDAC=32^(@) and angleAOB=70^(@) , then angleDBC is equal to

The diagonals AC and BD of a cyclic quadrilateral ABCD intersect each other at the point P. Then,it is always true that

In this figure angle DBC = 30^(@) and angle BCD = 110^(@) . Find angle BAC

Diagonals AC and BD of a parallelogram ABCD intersect each other at O. If OA= 3 cm and OD = 2 cm, determine the lengths of AC and BD.

Diagonals AC and BD of a trapezium ABCD with AB| DC intersect each other at O . Prove that ar(AOD)=ar(BOC)

diagonal of a cocyclic parallelogram ABCD is AC and BD intersection at point R .then

The diagonals of a quadrilateral ABCD intersect each other at the point O such that (AO)/(BO)=(CO)/(DO) Show that ABCD is a trapezium.