Home
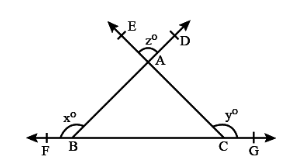
Class 9
MATHS
In the given figure, two rays BD and CE ...

In the given figure, two rays `BD` and `CE` intersect at a point `A.` The side `BC` of `DeltaABC` have been produced on both sides to points `F` and `G` respectively. If `angleABF=x^(@),angleACG=y^(@)andangleDAE=z^(@)" then "z=?`

A

`x+y-180`

B

`x+y+180`

C

`180-(x+y)`

D

`x+y+360^(@)`

Text Solution

Verified by Experts

The correct Answer is:
A
`angleBAC=angleEAD=z^(@),angleABC=(180^(@)-x^(@)),angleBCA=(180^(@)-y^(@))`,
`angleBAC+angleABC+angleBCA=180^(@)`
`impliesz+(180-x)+(180-y)=180impliesz=(x+y)-180^(@)`.
Promotional Banner

Topper's Solved these Questions

  • TRIANGLES

    RS AGGARWAL|Exercise Multiple Choice Questions (Mcq)|2 Videos

  • QUADRILATERALS

    RS AGGARWAL|Exercise Matching of Columns:|2 Videos

  • VOLUME AND SURFACE AREA OF SOLIDS

    RS AGGARWAL|Exercise Multiple Choice Questions (Mcq)|73 Videos

Similar Questions

Explore conceptually related problems

In the given figure, lines AB and CD intersect at a point O. The sides CA and OB have been produced to E and F respectively such that angleOAE=x^(@)andangleDBF=y^(@) If angleOCA=80^(@),angleCOA=40^(@)andangleBDO=70^(@)" then "x^(@)+y^(@)=?

Side BC of DeltaABC has been produced to a point D. If angleA=3y^(@),angleB=x^(@),angleC=5y^(@)andangleACD=7y^(@) . Then, the value of x is

In the given figure, the two lines AB and CD intersect at a point O such that angleBOC=125^(@) . Find the values of x, y, and z.

In the given figure, the sides AB and AC of DeltaABC have been extended to D and E respectively. If xgty , show that ABgtAC .

In Figure,the sides BC,CA and AB of a ABC have been produced to D,E and F respectively.If /_ACD=105^(@) and /_EAF=45^(@), find all the angles of the ABC

In the given figure, D and E are points on the side BC of a DeltaABC such that BD = CE and AD = AE. Show that DeltaABD~=DeltaACE.

In the adjoining figure, X and Y are respectively two points on equal sides AB and AC of DeltaABC such that AX = AY. Prove that CX = BY.

In the given figure, D is a point on side BC of a DeltaABC and E is a point such that CD = DE. Prove that AB+ACgtBE .

In the given figure, D and E are the points on the base BC of DeltaABC such that BD=CE, AD= AE and angleADE=angleAED , prove that DeltaADB cong DeltaAEC .