Text Solution
Verified by Experts
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
RS AGGARWAL-CIRCLES-Test Yourself
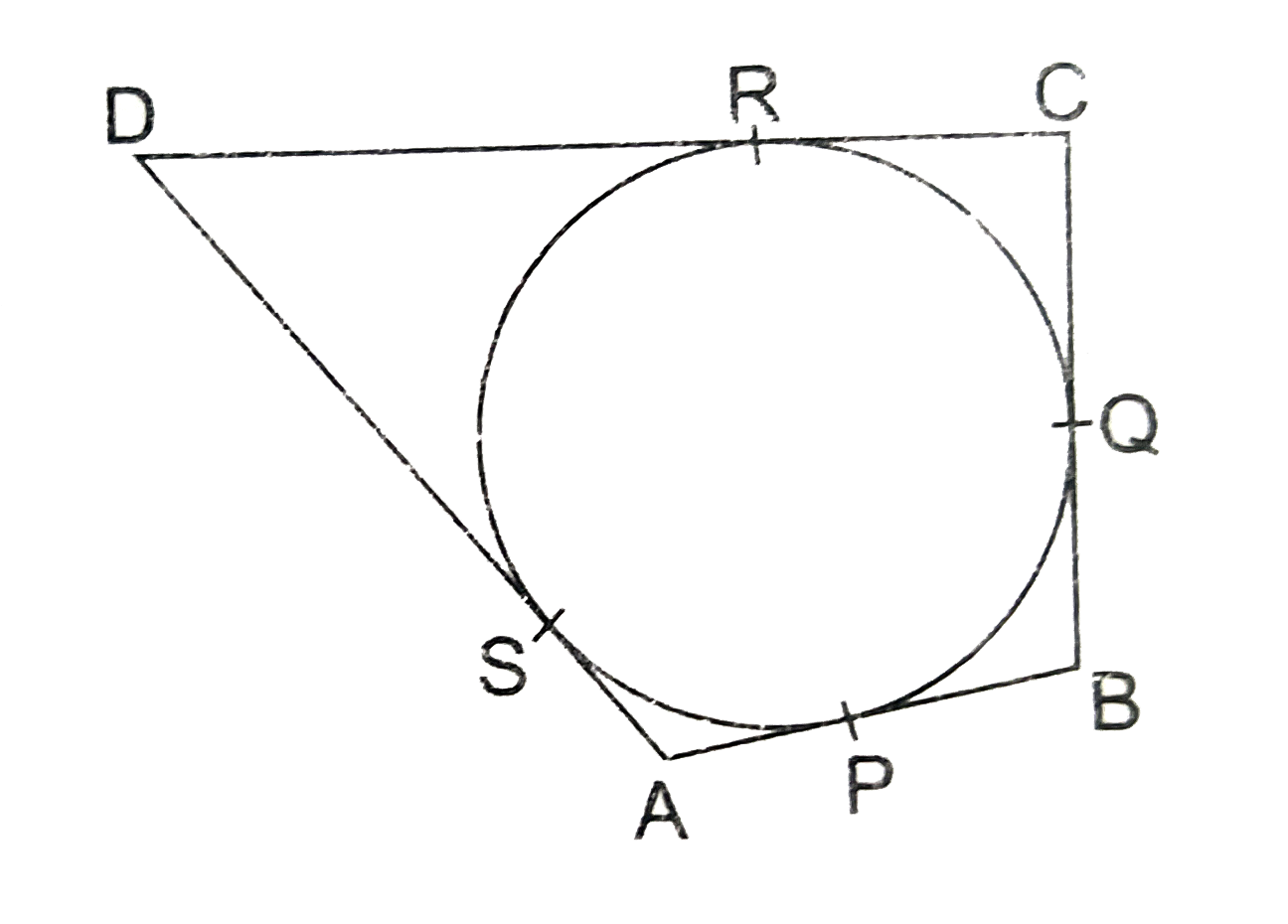
- A quadrilateral ABCD is drawn to circumscribe a circle, as shown in th...
Text Solution
|
- In the given figure ,'O is the centre of circle ,PQ is a chord and the...
Text Solution
|
- If the angle between two radii of a circle is 130^(@) then the angle b...
Text Solution
|
- If tangents PA and PB from a point P to circle with centre O drawn so ...
Text Solution
|
- In the given figure, AD and AE are the tangents to a circle with centr...
Text Solution
|
- In the given figure, a quadrilateral ABCD is drawn to circumscribe a c...
Text Solution
|
- In the given figure, PA and PB are the tangents to a circle with centr...
Text Solution
|
- In the given figure, PA and PB are two tangents from an external point...
Text Solution
|
- Two tangent segments BC and BDare drawn to a circle with centre O such...
Text Solution
|
- Fill in the blanks (i) A line intersecting a circle in two distinct ...
Text Solution
|
- Prove that the length of the tangents drawn from an external point to ...
Text Solution
|
- Prove that the tangents drawn at the ends of the diameter of a circle ...
Text Solution
|
- In the given figure, if AB=AC, prove that BE=CE.
Text Solution
|
- Theorem:If two tangents are drawn to a circle from an external point ;...
Text Solution
|
- Prove that the tangents drawn at the end points of a chord of a circle...
Text Solution
|
- सिद्ध कीजिए कि किसी वृत्त के परिगत समांतर चतुर्भुज समचतुर्भुज होता है...
Text Solution
|
- Two concentric circles are of radii 5cm and 3cm respectively. Find the...
Text Solution
|
- एक वृत्त के परिगत एक चतुर्भुज ABCD खींचा गया है सिद्ध कीजिए AB +CD =...
Text Solution
|
- Prove that opposite sides of a quadrilateral circumscribing a circle s...
Text Solution
|
- Prove that the angle between the two tangents drawn from an external ...
Text Solution
|
- PQ is a chord of length 16cm of a circle of radius 10cm. The tangents ...
Text Solution
|