Home
Class 10
MATHS
In the given figure, PQ is a chord of a ...

In the given figure, `PQ` is a chord of a circle with centre `O` and `PT` is a tangent. If `/_QPT=60^(@)`, find `/_PRQ`.

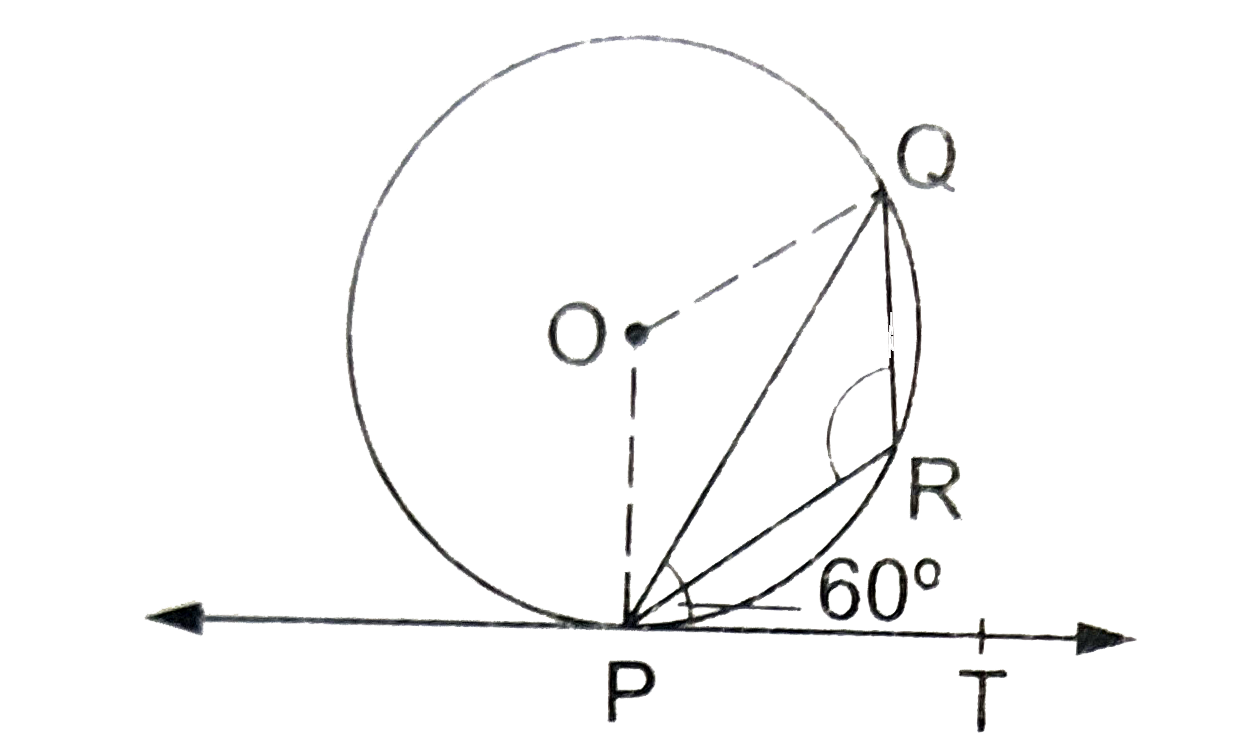
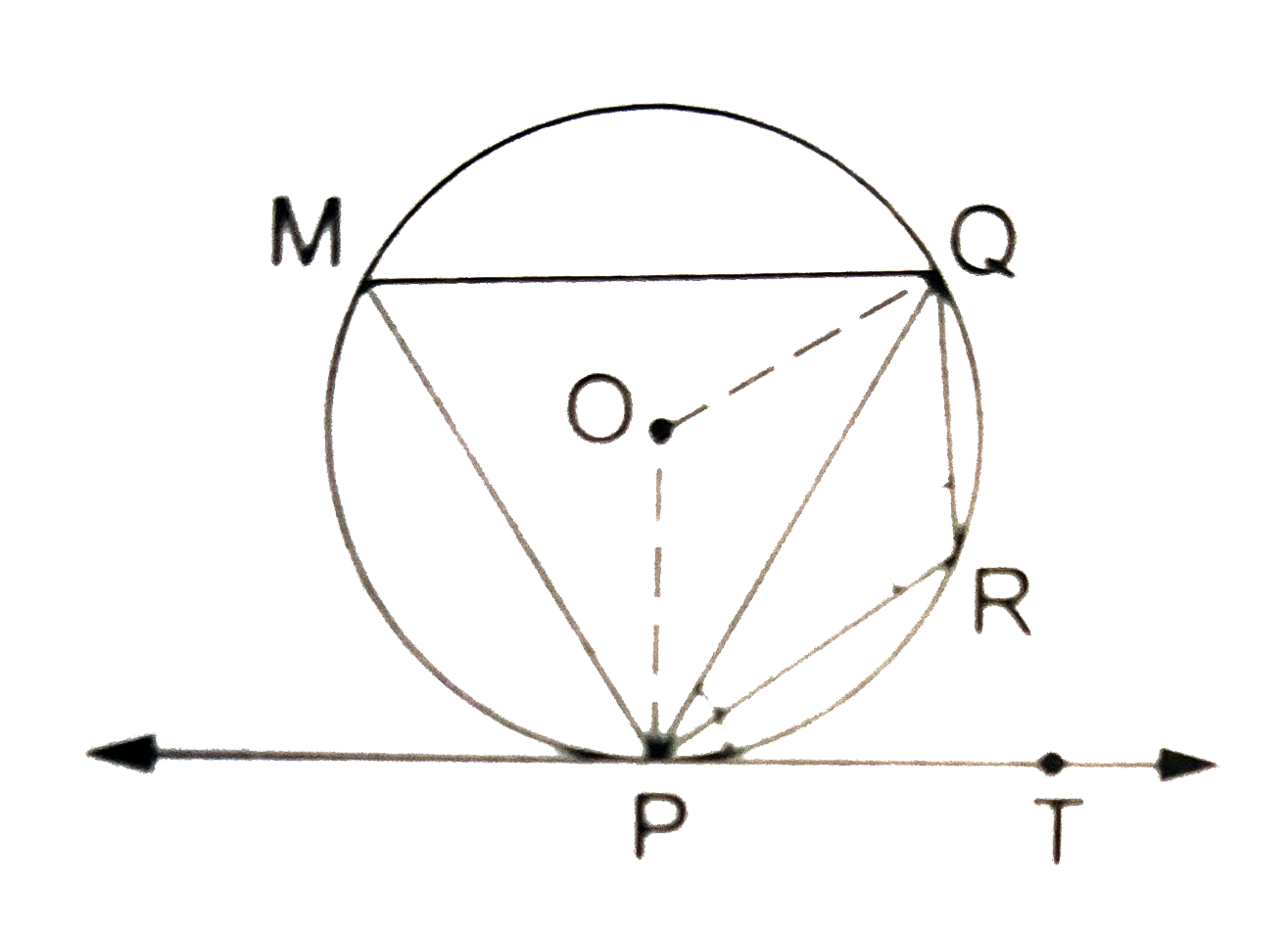
Text Solution

Verified by Experts

Mark a point `M` in the alternate segment.
Join `MP` and `MQ`.
Then, `/_PMQ=/_QPT=60^(@)` [angles in the alternate segments]
Now, `/_PMQ+/_PRQ=180^(@)` [`:'PMQR` is cyclic quadrilateral]
`implies/_PRQ=180^(@)-/_PMQ=180^(@)-60^(@)=120^(@)`.
Promotional Banner

Topper's Solved these Questions

  • CIRCLES

    RS AGGARWAL|Exercise Multiple Choice Questions (Mcq)|15 Videos

  • CIRCLES

    RS AGGARWAL|Exercise Multiple-choice questions (MCQ)|39 Videos

  • CIRCLES

    RS AGGARWAL|Exercise Exercise 8A|16 Videos

  • ARITHMETIC PROGRESSION

    RS AGGARWAL|Exercise Multiple Choice Questions (Mcq)|30 Videos

  • CONSTRUCTIONS

    RS AGGARWAL|Exercise Test Yourself|10 Videos

Similar Questions

Explore conceptually related problems

In Figure PQ is a chord of a circle with centre O and PT is a tangent. If QPT =60^@ so, find PRQ.

In the figure,PQ is a chord of a circle with centre O and PT is the tangent at P such that /_QPT=70^(@). Then the measure of /_PRQ is equal to : (A) 135^(@) (B) 150^(@) (C) 120^(@) (D) 110^(@)

In the given figure, AB is a tangent to a circle with centre O. Prove angle BPQ = angle PRQ .

In the adjoining figure, PQ is a chord of a circle and PT is the tangent at P such that angleQPT=60^(@). Find anglePRQ.

In the given figure,AB is a tangent to a circle with centre.Prove that /_BPQ=/_PRQ If /_BPQ=60^(@), find /_RPQ.

In the given figure,PQ is tangent at a point R of the circle with centre O.If,find m/_PRS .