Home
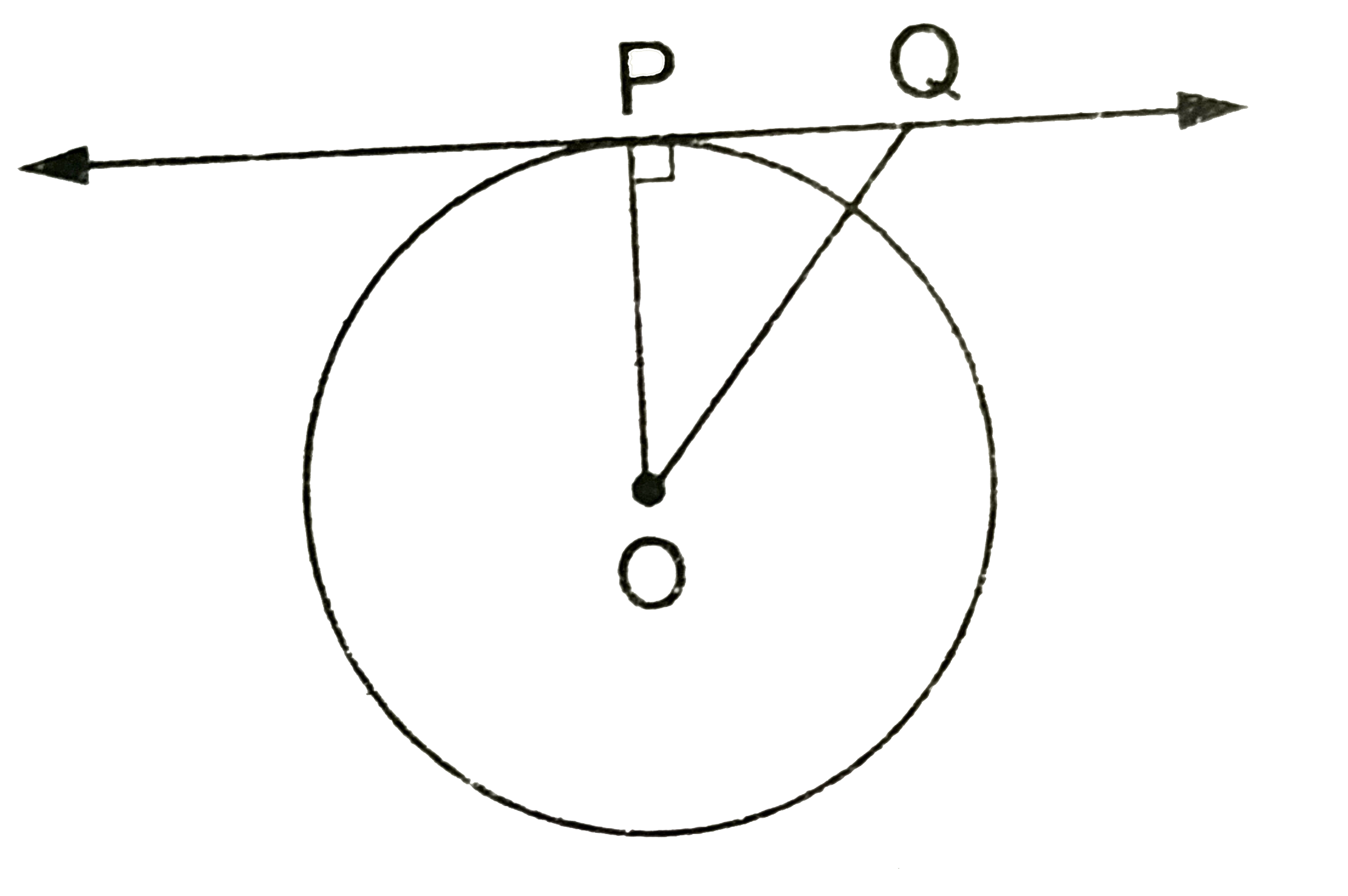
Class 10
MATHS
PQ is a tangent to a circle with centre ...

`PQ` is a tangent to a circle with centre `O` at the point `P`. If `DeltaOPQ` is an isoceless triangle, then `/_OQP` is equal to

A

`30^(@)`

B

`45^(@)`

C

`60^(@)`

D

`90^(@)`

Text Solution

Verified by Experts

We have `OPbotPQ`, i.e., `/_OPQ=90^(@)`
`DeltaOPQ` is isosceles `impliesOP=PQimplies/_OQP=/_POQ=45^(@)`
[`:'` in a triangle, angles opposite equal sides are equal].
Promotional Banner

Topper's Solved these Questions

  • CIRCLES

    RS AGGARWAL|Exercise Multiple-choice questions (MCQ)|39 Videos

  • CIRCLES

    RS AGGARWAL|Exercise Assertion-and-Reason|1 Videos

  • CIRCLES

    RS AGGARWAL|Exercise Exercise 8B|15 Videos

  • ARITHMETIC PROGRESSION

    RS AGGARWAL|Exercise Multiple Choice Questions (Mcq)|30 Videos

  • CONSTRUCTIONS

    RS AGGARWAL|Exercise Test Yourself|10 Videos

Similar Questions

Explore conceptually related problems

PQ is a tangent to a circle with centre O at the point P. If OPQ is an isosceles triangle, then /_OQP is equal to 30o (b) 45o(c)600 (d) 90o

If two tangents are inclined at 60^(@) are drawn to a circle of radius 3cm then find length of each tangent. OR PQ is a tangent to a circle with centre O at point P. If Delta OPQ is an isosceles triangle, then find angle OQP.

In figure-3, PQ is tangent to the circle with centre at O, at the point B. if angleAOB=100^(@) , then angleABP is equal to

In figure PQ is tangent to the circle with centre at O at the point B , if angle AOB = 100^(@) , then angle ABP is equal to

If tangents PA and PB from a point P to a circle with centre O are inclined to each other at angle of 80o , then /_P O A is equal to

PA and PB are tangents to a circle with centre O from point P.OP is equal to the diameter of the circle.Prove that ABP is equilateral triangle,

If tangents PA and PB from a point P to a circle with centre O are inclined to each other at an angle of 70^(@) , then /_POA is equal to