Similar Questions
Explore conceptually related problems
Recommended Questions
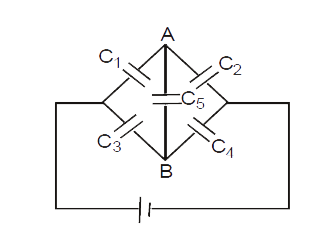
- Find out the Relation between C1, C2, C3 and C4 such that point A and ...
Text Solution
|
- If the lines whose equations are y=m1 x+ c1 , y = m2 x + c2 and y=m3 x...
Text Solution
|
- Find out the Relation between C1, C2, C3 and C4 such that point A an...
Text Solution
|
- C0 C1+C1 C2 + C2 C3+…+ C(n-1) Cn=
Text Solution
|
- Find out the Relation between C1, C2, C3 and C4 such that point A and ...
Text Solution
|
- If C1, C2 , C3 , C4 are the coefficients of any consecutive terms in t...
Text Solution
|
- (.^21 C1- .^10 C1) + (.^21 C2- .^10 C2) + (.^21 C3- .^10 C3) + (.^21 C...
Text Solution
|
- Prove that (C0+C1)(C1+C2)(C2+C3)(C3+C4)...........(C(n-1)+Cn) = (C0...
Text Solution
|
- Consider three circles C1, C2 and C3 such that C2 is the director circ...
Text Solution
|