Similar Questions
Explore conceptually related problems
Recommended Questions
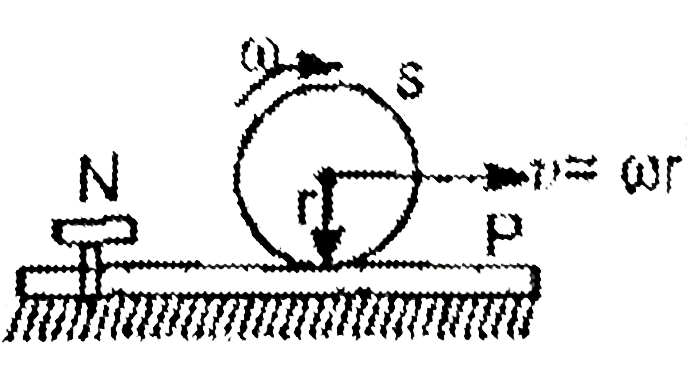
- A sphere S rolls without slipping moving with a constant speed on a pl...
Text Solution
|
- A ball is given a velocity v and angular velocity such that the ball r...
Text Solution
|
- A hoop rolls on a horizontal ground without slipping with linear speed...
Text Solution
|
- A cylinder is rolling without slipping on a horizontal plane P. The fr...
Text Solution
|
- A ring rolls without slipping on the ground. Its centre C moves with a...
Text Solution
|
- A wheel of radius R=0.1m is rolling without slipping on a horizontal s...
Text Solution
|
- A sphere S rolls without slipping moving with a constant speed on a pl...
Text Solution
|
- A solid sphere is rolling without slipping on rough ground as shown in...
Text Solution
|
- Assertion : A solid sphere cannot roll without slipping on smooth hori...
Text Solution
|