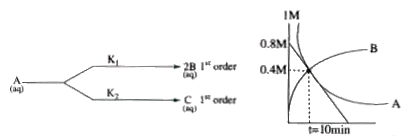Home
Class 12
CHEMISTRY
What is the ratio of the rate constants ...


What is the ratio of the rate constants `K_(1)` and `K_(2)` ?

A

`2:3`

B

`1:3`

C

`2:5`

D

`1:2`

Text Solution

Verified by Experts

The correct Answer is:
D
`K=K_(1)+K_(2)`……..(1),`y_(B)=y_(A)=0.4`………2 , `y_(C)=K_(2)//K`……3
from 1, 2, 3, `K_(1),K_(2)=1:2`
Promotional Banner

Topper's Solved these Questions

  • CHEMICAL KINETICS

    AAKASH SERIES|Exercise PRACTICE SHEET-5 (MATCH THE FOLLOWING QUESTIONS)|2 Videos

  • CHEMICAL KINETICS

    AAKASH SERIES|Exercise PRACTICE SHEET-5 (INTEGER ANSWER TYPE QUESTIONS)|6 Videos

  • CHEMICAL KINETICS

    AAKASH SERIES|Exercise PRACTICE SHEET-5 (SINGLE OR MORE THAN ONE OPTION QUESTIONS)|16 Videos

  • CHEMICAL KINETCS

    AAKASH SERIES|Exercise EXERCISE - 3.2|45 Videos

  • CHEMICAL THERMODYNAMICS

    AAKASH SERIES|Exercise Additional Practice Exercise|54 Videos

Similar Questions

Explore conceptually related problems

A to B and C to D are first order reactions. Ratio of t_(99.9%) values is 4:1, then, ratio of rate constants K_1 to K_2 is

Write the equation which ralates th rate constants k_(1)and k_(2) at temperatures T_(1) and T_(2) of a reaction.

For reaction AtoB the rate constant k_(1)=A_(1)e^(-Ea_(1)//RT) and for the reaction PtoQ the rate constant k_(2)=A_(2)e^(-Ea_(2)//RT) . If A_(1)=10^(8),A_(2)=10^(10) and E_(a_(1))=600,E_(a_(2))=1200 , then the temperature at which k_(1)=k_(2) is

Two bodies A and B of equal masses are suspended from two separate massless springs of force constants K_(1) and K_(2) . If they oscillate vertically so that their maximum velocities are equal the ratio of their amplitudes is

The instantaneous rate of an elementary chamical reactkon aA+bBhArr cC+dD can be given by rate =K_(f)[A]^(a)[B]^(b)-K_(b)[C]^(c)[D]^(d) where K_(f) and K_(b) are rate constants for forward and backward reactions respectively for the reversible reaction. If the reaction is an irreversible one, the rate is expressed as, rate =K[A]^(a)[B]^(b) where K is rate contant for the given irreversible rate of disappearance of A is a/b times the rate of disappearance of B. The variation of rate constant K with temperature is expressed in terms of Arrhenius equation: K=Ae^(-E_(a)//RT) whereas the ratio (K_(f))/(K_(b)) is expressed in terms of van't Hoff isochore: (K_(f))/(K_(b))=Ae^(-DeltaH//RT) , where E_(a) and DeltaH are energy of activation and heat of reaction respectively. The variation of rate constant K and (K_(f))/(K_(b)) with temperature shows the following effects: For endothrmic reaction when T increases then K increases and (K_(f))/(K_(b)) also increases. (ii) For endothemic reaction when T decreases then K decreases and (K_(f))/(K_(b)) also decreases. (iii) For exothermic when T increases then K and (K_(f))/(K_(b)) both increases. (iv) For exothermic reaction when T decreases then K increases and (K_(f))/(K_(b)) decrease. (v) For exothermic reaction when T increases thenK and (K_(f))/(K_(b)) both decrease.