Similar Questions
Explore conceptually related problems
Recommended Questions
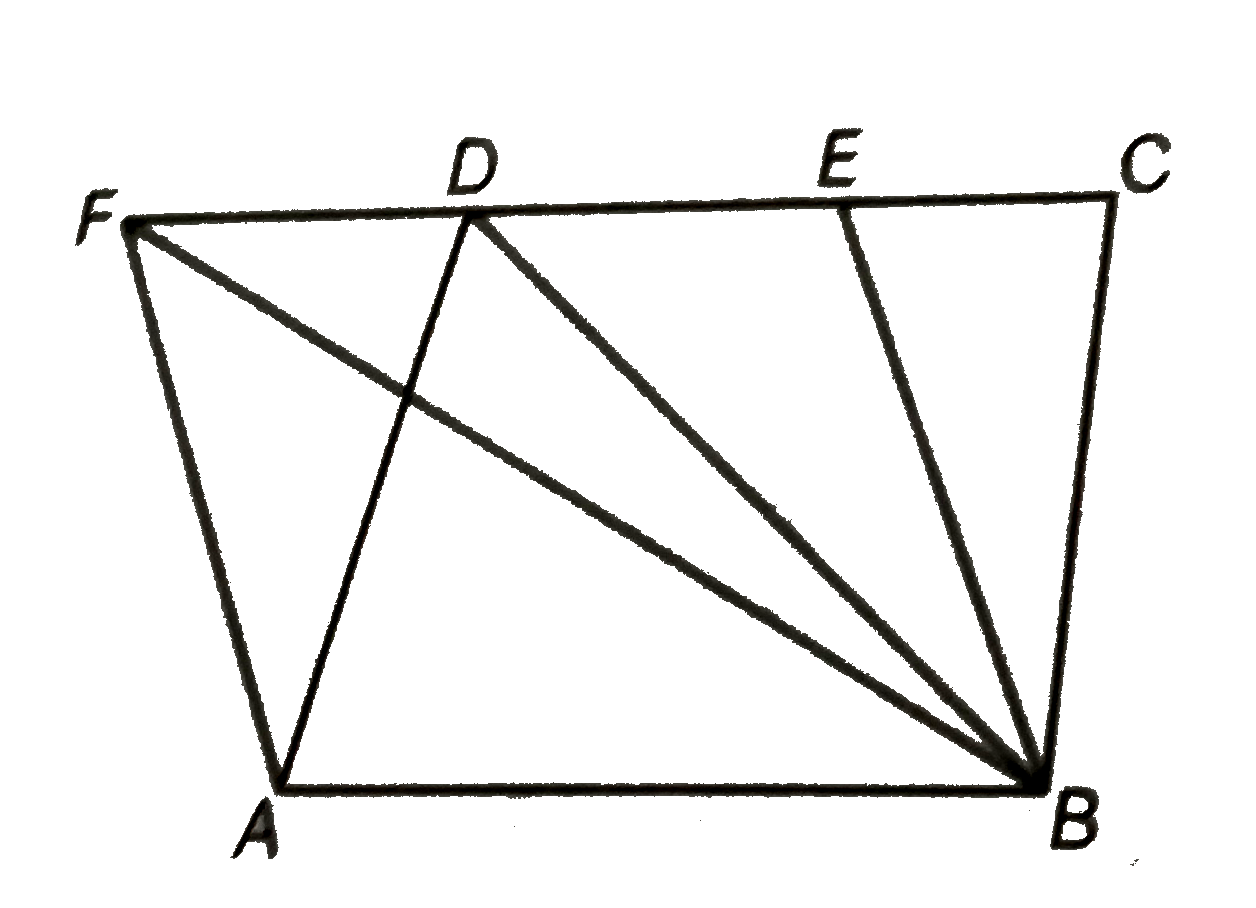
- The area of the parallelogram ABCD is 90 CM^(2). Find (i) ar (ABEF) ...
Text Solution
|
- The area of the parallelogram ABCD is 90 CM^(2). Find (i) ar (ABEF) ...
Text Solution
|
- Determine the point of symmetry of a regular hexagon. <img src="htt...
Text Solution
|
- Match the following Column A to Column B
Text Solution
|
- Match the following Column A to Column B
Text Solution
|
- Match the following Column A to Column B
Text Solution
|
- Find the area of figure given below.
Text Solution
|
- Find the area of the figure given below.
Text Solution
|
- In the figure given above, ABCD is a quadrilateral and BPDQ is paralle...
Text Solution
|