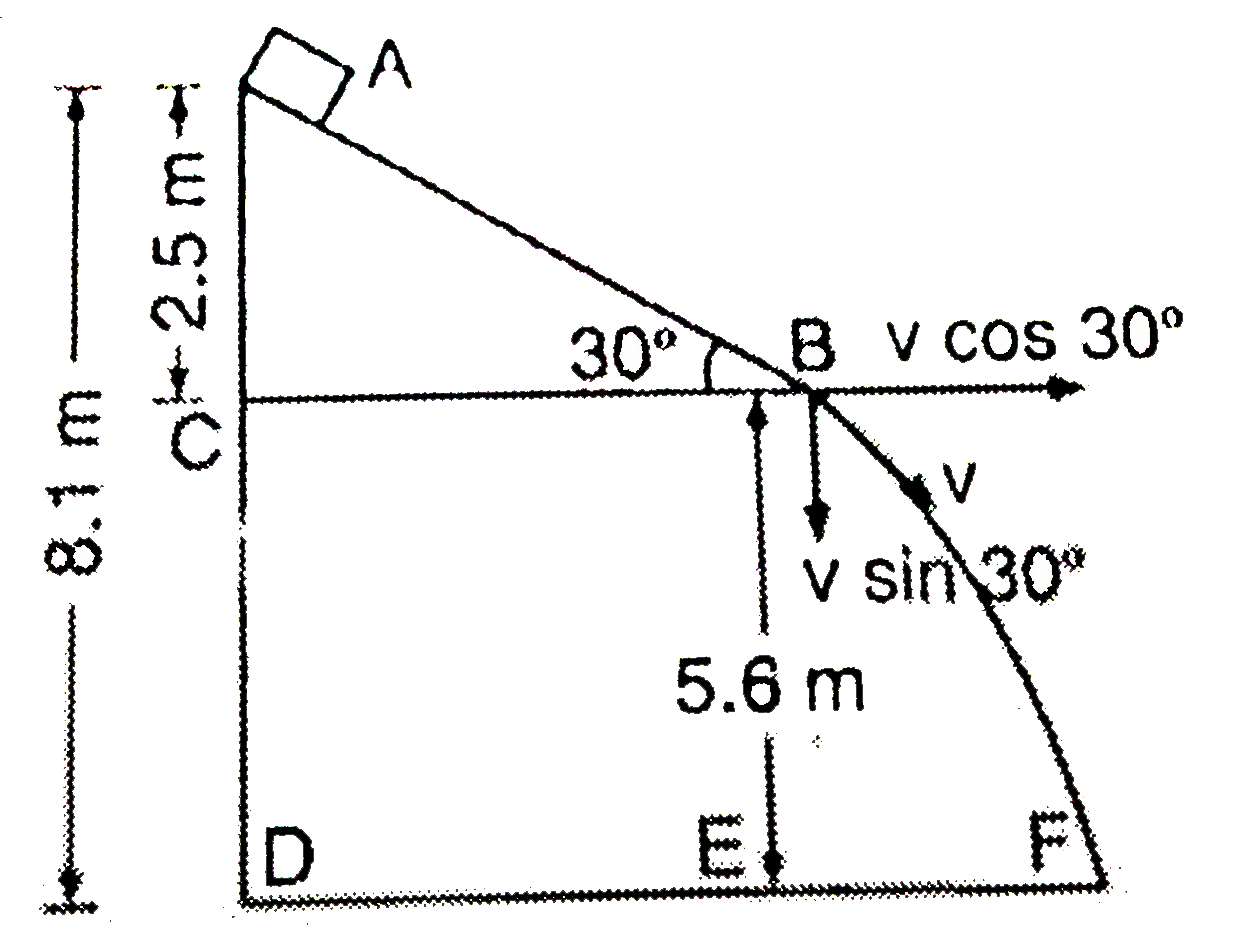Similar Questions
Explore conceptually related problems
Recommended Questions
- A block of ice starts sliding down from the top of the inclined roof o...
Text Solution
|
- A block slides down an inclined surface of inclination 30^0 with the h...
Text Solution
|
- A block slides down an incline of 30^(@) with the horizontal starting ...
Text Solution
|
- A block is at rest on an inclined plane making an angle alpha with the...
Text Solution
|
- A block is pushed upwards along the roof forming an angle a with the h...
Text Solution
|
- A block of ice starts sliding down from the top of the inclined roof o...
Text Solution
|
- A block of mass m rests on a rough inclined plane. The coefficient of ...
Text Solution
|
- एक नत समतल पर एक ब्लॉक रखा है | नत समतल का क्षैतिज से झुकाव कोण बढ़ाने ...
Text Solution
|
- एक मकान कि छत से मैदान में पड़े एक पत्थर का अवनमन कोण 60^(@) है। यदि ...
Text Solution
|