Similar Questions
Explore conceptually related problems
Recommended Questions
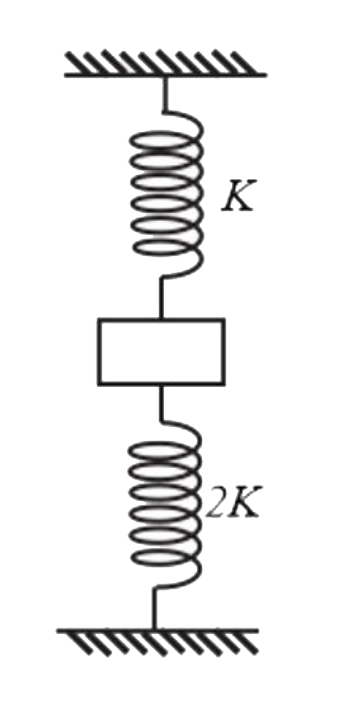
- A block of mass m is connected two springs of spring constant 2k annd ...
Text Solution
|
- A block of mass m is suddenly released from the top of a spring of sti...
Text Solution
|
- Two spring are connected toa block of mass M placed a frictionless sur...
Text Solution
|
- A block of mass m moving at a speed v0 compresses a spring of spring c...
Text Solution
|
- Two springs are in a series combination and are attached to a block of...
Text Solution
|
- A block tied between two identical springs is in equilibrium. If upper...
Text Solution
|
- If the lower spring is cut, find acceleration of the blokcs, immediate...
Text Solution
|
- A block of mass m is connected two springs of spring constant 2k annd ...
Text Solution
|
- Block of mass m=10kg is suspended by two springs vertically as shown i...
Text Solution
|