When a container open to atmmosphere , obtain the velocity of liquid coming out of the narrow hole from the wall of container by using Bernoulli's equation and obtain Torricelli's law

Explanation

Torricelli.s discovered that speed of efflux from an open tank is given by a formula identical to that of a freely falling body .
Consider a tank containing a liquid of density `rho` with a small hole in its side at a height `y_(1)` from the bottom . the air above the liquid , whose surface is at height `y_(2)` is at pressure P.

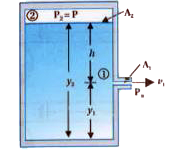
The velocities `v_(1)andv_(2)` are at point 1 and 2 respectively.
Using equation of continuity for points 1 and 2,
`A_(1)v_(1)=A_(2)v_(2)`
`v_(2)=(A_(1)v_(1))/(A_(2))` ..... (1)
`A_(2)` is the cross sectional area of the tank and
`A_(1)` is the cross sectional area of the hole
`A_(2)gtgtA_(1)` hence
`v_(2)ltltv_(1)thereforev_(2)=0`.
Using Bernoulli.s equation at 1 and 2
`P_(1)+(1)/(2)rhov_(1)^(2)+rhogy_(1)=P_(2)+(1)/(2)rhov_(2)^(2)+rhogy_(2)`
Here `P_(1)=` atmospheric pressure `P_(a)`
`P_(2)=P`
`v_(2)=0`
`P_(a)+(1)/(2)rhov_(1)^(2)+rhogy_(1)=P+rhogy_(2)`
`therefore(1)/(2)rhov_(1)^(2)=(P-P_(a))+rhog(y_(2)-y_(1))`
Taking h as the difference in height `=y_(2)-y_(1)(1)/(2)rhov_(1)^(2)=(P-P_(a))+rhogh`
`v_(1)=sqrt(2gh+(2(P-P_(a)))/(rho))` .... (2)
Special Cases : `(1)PgtgtP_(a),2gh` is neglecting with the value of `(P-P_(a))`.
`thereforev_(1)=sqrt((2(P-P_(a)))/(rho))` ....(3)
Hence , the speed of efflux determined only by the pressure of container . Such a situation occurs in rocket propulsion where efflux means coming out liquid.
(2) If the tank is open to atmosphere , then
`P=P_(a)` and equation (2) becomes as below.
`v_(1)=sqrt(2gh)` .... (4)
This is the speed of a freely falling body . This equation is known as Torricelli.s law.