Give the definition of surface tension and formula in the context of (i) inter molecular forces (ii) potential energy (iii) work done.

Explanation

In below figure a free surface of liquid is shown A line of unit length in the middle of the surface except near to wall is shown . The force exerted on both side of line, perpendicular to line and parallel to the surface . If length of line is l and force F, then surface tension `S=(F)/(l)`.
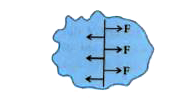(i) Figure shown , on free surface of liquid if a line of unit length is out then the molecules one of side of line exert force on the molecules of other side of line perpendicular to the line and parallel to the surface then this force is known as surface tension (S). Here length
`S=(F)/(l)(("Newton")/("meter"))`
(ii) The potential energy stored per unit area of a free surface of liquid is known as surface tension of liquid.
`S=(E)/(A)(("Joule")/("metre")=("Newton"xx"metre")/("metre"^(2))=("Newton")/("metre"))`
(iii) The work done to increase the unit surface area of a liquid is equal to the surface tension.
`S=(W)/(DeltaA)(("Joule")/("metre"^(2))=("Newton")/("metre"))`
(Note : surface tension is denoted by T.)