Text Solution
Verified by Experts
Topper's Solved these Questions
OSCILLATIONS
KUMAR PRAKASHAN|Exercise SECTION-B (NUMERICAL FROM TEXTUAL EXERCISE)|48 VideosOSCILLATIONS
KUMAR PRAKASHAN|Exercise SECTION-B (ADDITIONAL EXERCISE)|9 VideosOSCILLATIONS
KUMAR PRAKASHAN|Exercise SECTION-A (TRY YOURSELF)|64 VideosOBJECTIVE QUESTIONS AS PER NEW PAPER STYLE
KUMAR PRAKASHAN|Exercise CHAPTER - 8 (Match Type questions)|5 VideosPHYSICAL WORLD
KUMAR PRAKASHAN|Exercise SECTION-E (QUESTIONS FROM MODULE)|9 Videos
Similar Questions
Explore conceptually related problems
KUMAR PRAKASHAN-OSCILLATIONS-SECTION-B (NUMERICAL FROM TEXTUAL ILLUSTRATIONS)
- A body oscillator with SHM according to the equation (in SI units) x...
Text Solution
|
- A body oscillator with SHM according to the equation (in SI units) x...
Text Solution
|
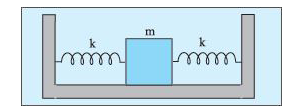
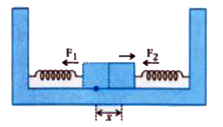
- Two identical springs of spring constant k are attached to a block of ...
Text Solution
|
- A block whose mass is 1kg is fastened to a spring. The spring has a sp...
Text Solution
|
- A block whose mass is 2kg is fastened to a spring. The spring has a sp...
Text Solution
|
- A block whose mass is 1kg is fastened to a spring. The spring has a sp...
Text Solution
|
- A 5kg collar is attached to a spring of spring constant 500 Nm^(-1). I...
Text Solution
|
- A 5 kg collar is attached to a spring of spring constant 500 N m^(-1)....
Text Solution
|
- A 5 kg collar is attached to a spring of spring constant 500 N m^(-1)....
Text Solution
|
- A 2kg collar is attached to a spring of spring constant 800 Nm^(-1). I...
Text Solution
|
- A 2kg collar is attached to a spring of spring constant 800 Nm^(-1). I...
Text Solution
|
- A 2kg collar is attached to a spring of spring constant 800 Nm^(-1). I...
Text Solution
|
- What is the length of a simple pendulum, which ticks seconds ?
Text Solution
|
- How much will the length of a simple pendulum be if its time period is...
Text Solution
|
- What would be the length of a simple pendulum on Moon if we get its pe...
Text Solution
|
- What will be the time period of seconds pendulum if its length is doub...
Text Solution
|
- For the damped oscillator, the mass m of the block is 200g, k = 90 Nm^...
Text Solution
|
- For the damped oscillator, the mass m of the block is 200g, k = 90 Nm^...
Text Solution
|
- For the damped oscillator, the mass m of the block is 200g, k = 90 Nm^...
Text Solution
|
- For the damped oscillator, the mass m of the block is 400g, k = 120 Nm...
Text Solution
|