Text Solution
Verified by Experts
Topper's Solved these Questions
OSCILLATIONS
KUMAR PRAKASHAN|Exercise SECTION-B (ADDITIONAL EXERCISE)|9 VideosOSCILLATIONS
KUMAR PRAKASHAN|Exercise SECTION-B (NUMERICAL FROM DARPAN BASED ON TEXTBOOK)|15 VideosOSCILLATIONS
KUMAR PRAKASHAN|Exercise SECTION-B (NUMERICAL FROM TEXTUAL ILLUSTRATIONS)|40 VideosOBJECTIVE QUESTIONS AS PER NEW PAPER STYLE
KUMAR PRAKASHAN|Exercise CHAPTER - 8 (Match Type questions)|5 VideosPHYSICAL WORLD
KUMAR PRAKASHAN|Exercise SECTION-E (QUESTIONS FROM MODULE)|9 Videos
Similar Questions
Explore conceptually related problems
KUMAR PRAKASHAN-OSCILLATIONS-SECTION-B (NUMERICAL FROM TEXTUAL EXERCISE)
- A spring having with a spring constant 1200 N m^(-1) is mounted on a h...
Text Solution
|
- A spring having with a spring constant 1200 N m^(-1) is mounted on a h...
Text Solution
|
- In Exercise 9, let us take the position of mass when the spring is un...
Text Solution
|
- In Exercise 9, let us take the position of mass when the spring is un...
Text Solution
|
- In Exercise 9, let us take the position of mass when the spring is un...
Text Solution
|
- Figures 14.25 correspond to two circular motions. The radius of the ci...
Text Solution
|
- Plot the corresponding reference circle for each of the following simp...
Text Solution
|
- Plot the corresponding reference circle for each of the following simp...
Text Solution
|
- Plot the corresponding reference circle for each of the following simp...
Text Solution
|
- Plot the corresponding reference circle for each of the following simp...
Text Solution
|
- Figure 14.26 (a) shows a spring of force constant k clamped rigidly at...
Text Solution
|
- The piston in the cylinder head of a locomotive has a stroke (twice th...
Text Solution
|
- The acceleration due to gravity on the surface of moon is 1.7 m s^(-2)...
Text Solution
|
- Answer the following question : Time period of a particle in SHM dep...
Text Solution
|
- Answer the following question : The motion of a simple pendulum is a...
Text Solution
|
- Answer the following question : A man with a wristwatch on his hand ...
Text Solution
|
- Answer the following question : What is the frequency of oscillation...
Text Solution
|
- A simple pendulum of length l and having a bob of mass M is suspended ...
Text Solution
|
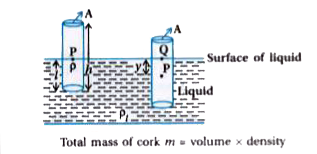
- A cylindrical piece of cork of density of base area A and height h flo...
Text Solution
|
- One end of a U-tube containing mercury is connected to a suction pump ...
Text Solution
|