Text Solution
Verified by Experts
Topper's Solved these Questions
OSCILLATIONS
KUMAR PRAKASHAN|Exercise SECTION-D (NCERT EXEMPLAR SOLUTION SHORT ANSWER QUESTIONS)|6 VideosOSCILLATIONS
KUMAR PRAKASHAN|Exercise SECTION-D (NCERT EXEMPLAR SOLUTION LONG ANSWER QUESTIONS)|8 VideosOSCILLATIONS
KUMAR PRAKASHAN|Exercise SECTION-D (NCERT EXEMPLAR SOLUTION MCQs MORE THAN ONE OPTIONS)|8 VideosOBJECTIVE QUESTIONS AS PER NEW PAPER STYLE
KUMAR PRAKASHAN|Exercise CHAPTER - 8 (Match Type questions)|5 VideosPHYSICAL WORLD
KUMAR PRAKASHAN|Exercise SECTION-E (QUESTIONS FROM MODULE)|9 Videos
Similar Questions
Explore conceptually related problems
KUMAR PRAKASHAN-OSCILLATIONS-SECTION-D (NCERT EXEMPLAR SOLUTION VERY SHORT ANSWER QUESTIONS)
- Displacement versus time curve for a particle executing SHM is shown i...
Text Solution
|
- Two identical springs of spring constant k are attached to a block of ...
Text Solution
|
- What are the two basic characteristics of a simple harmonic motion?
Text Solution
|
- When will the motion of a simple pendulum be simple harmonic?
Text Solution
|
- Obtain the ratio of maximum acceleration and maximum velocity of a SHM...
Text Solution
|
- What is the ratio between the distance travelled by the oscillator in ...
Text Solution
|
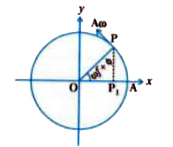
- In the figure, what will be the sign of the velocity of the point P1, ...
Text Solution
|
- Show that for a particle executing SHM, velocity and displacement have...
Text Solution
|
- Draw a graph to show the variation of PE, KE and total energy of a sim...
Text Solution
|
- The length of a second's pendulum on the surface of earth is 1m. What ...
Text Solution
|
 .
. .
.