A simple pendulum of time period 1s and length l is hung from a fixed support at 0. Such that the bob is at a distance H vertically above A on the ground (figure) the amplitude is `theta_(0)` the string snaps at `theta =(theta_0)/(2)`. Find the time taken by the bob to hit the ground. Also find distance from A where bob hits the ground. Assume `theta_(0)` to be small, so that `sin theta_(0) approx theta_(0)" and"cos theta_(0) approx 1`.
.

Explanation

Two components of velocity
Perpendicular component to the string `v_(y)= l omega sin ""(theta_0)/(2)`
Prallel component to the string `v_(x)= l omega cos (theta_0)/(2)`

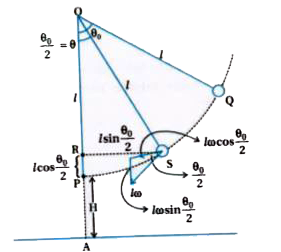
From `v= r omega`
`therefore v= l omega`
Suppose at `t=0, theta = theta_0`
`therefore theta = theta_(0) cos omega t`
but `T= 1s, therefore omega (2pi)/(T)= 2pi rad"/"s`
`therefore theta= theta_(0) cos 2pi t" ""........"(1)`
Now at `t= t_(1)` time, `theta= (theta_0)/(2)`
`therefore (theta_0)/(2)= theta_(0) cos 2pi t_(1)`
`therefore (1)/(2) = cos 2pi t_(1)`
`therefore 2pi t_(1) = (pi)/(3)`
`therefore t_(1)= (1)/(6)s`
Difference equation (1) with time,
`(d theta)/(dt)= -theta_(0) 2pi sin 2pi t`
`therefore t= t_(1)` time
`omega = -2pi theta_(0) xx sin 2pi xx (1)/(6)`
`=-2pi theta_(0) xx sin ""(pi)/(3)`
`= -2pi theta_(0) xx sin"" (sqrt(3))/(3)`
`therefore omega = -sqrt(3) pi theta_(0)`
(-)ve shows that bob.s motion is towards, left. Since linear velocity is in the tangential direction.
`therefore v= l omega" "[therefore v= A omega]`
`therefore v= -sqrt(3) pi theta_(0) l`
The Y-component of linear velocity
`v_(y)= -sqrt(3) pi theta_(0) l sin ""(theta_0)/(2)` and x-component of velocity
`v_(x)= -sqrt(3) pi theta_(0) l cos"" (theta_0)/(2)`
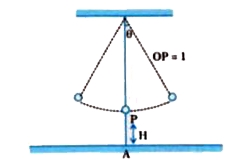
When string break, the height of bob from the ground,
`H. = H+l(1- cos ""(theta_0)/(2))" ""........"(2)`
Time taken by the bob from this height (when string break) to ground it t, then
`H.= v_(y)t+(1)/(2)g t^(2)` (all terms are (-)ve)
`therefore (1)/(2) g t^(2) + sqrt(2) pi theta_(0) l sin ""(theta_0)/(2) l-H.=0` is a quadratic formula of t
`therefore triangle = b^(2) -4ac`
`=3p^(2)theta_(0)^(2)sin^(2) ""(theta_0)/(2)+4xx(1)/(2)gxx H.`
`=3pi^(2) theta_(0)^(2) l^(2) sin^(2) ""(theta_0)/(2) + 2gH.`
but `theta_0` is small `therefore sin^(2) ""(theta_0)/(2)=0`, `triangle = 2gH.`
`therefore sqrt(triangle) = sqrt(2gH.)`
`therefore t= (-b pm sqrt(triangle))/(2a)`
`= (-sqrt(3) pi theta_(0) l sin ""(theta_0)/(2) pm sqrt(2gH.))/(2xx (1)/(2)g)`
but `sin""(theta_0)/(2)=0`,
`t= (pm sqrt(2gH.))/(g)`
`therefore t= sqrt((2H.)/(g))" ""........"(3)`
Now, in `H. = H+l(1-cos ""(theta_0)/(2)), theta_(0)` is small `cos ""(theta_2)/(2) approx 1`
`therefore H.= H+l(1-1)`
`therefore H.= H`
`therefore t= sqrt((2H)/(g))" "[" from equation (3) "]" ""........."(4)`
The bob covered distance in horizontal direction.
`X= v_(x) t`
`= -sqrt(3) pi theta_(0) l cos ""(theta_0)/(2)xx t`
Since `theta_(0)` is small, `cos ""(theta_0)/(2) approx 1` and taking `t= sqrt((2H)/(g))`,
`X= -sqrt(3) pi theta_(0) lxx sqrt((2H)/(g))`
`therefore X= -sqrt((6H)/(g))xx pi theta_(0) l" ""........"(5)`
but string breaks, the bob is at RS distance from vertical at that time and `RS= l sin ""(theta_0)/(2)`
`RS= (l theta_0)/(2)" "[therefore ""sin (theta_0)/(2) approx (theta_0)/(2)]`
When bob hit at ground, the distance from bob at that time
`=(l theta_0)/(2)+X`
`= (l theta_0)/(2) - sqrt((6H)/(g)) pi theta_(0) l`
`= theta_(0) l((1)/(2)-pi sqrt((6H)/(g)))`.