Text Solution
Verified by Experts
Topper's Solved these Questions
CURRENT ELECTRICITY
KUMAR PRAKASHAN|Exercise SECTION [B] (NUMERICAL FROM TEXTUAL EXERCISE)|35 VideosCURRENT ELECTRICITY
KUMAR PRAKASHAN|Exercise SECTION [B] (NUMERICAL FROM .DARPAN. BASED ON TEXTBOOK)|13 VideosCURRENT ELECTRICITY
KUMAR PRAKASHAN|Exercise SECTION [A] TRY YOURSELF|74 VideosBOARD'S QUESTION PAPER MARCH-2020
KUMAR PRAKASHAN|Exercise PART-B SECTION -C|4 VideosDUAL NATURE OF RADIATION AND MATTER
KUMAR PRAKASHAN|Exercise Section-D (MCQs asked in GUJCET/Board Exam)|1 Videos
Similar Questions
Explore conceptually related problems
KUMAR PRAKASHAN-CURRENT ELECTRICITY-SECTION [B] NUMERICALS (NUMERICAL FROM TEXTUAL ILLUSTRATIONS)
- (a) Esttimate the average drift speed of conduction electrons in a cop...
Text Solution
|
- In Example 3.1. the electron drift speed is estimated to be only a few...
Text Solution
|
- The electron drift arises due to the force experienced by electrons in...
Text Solution
|
- If the electron drift speed is small, and the electron's charge is sma...
Text Solution
|
- When electrons drift in a metal from lower to higher potential, does i...
Text Solution
|
- Are the paths of electrons straight lines between successive collision...
Text Solution
|
- An electric toaster uses nichrome for its heating element. When a negl...
Text Solution
|
- The resistance of the platinum wire of a platinum resistance thermomet...
Text Solution
|
- A network of resistore is connected to a 16 V battery with internal re...
Text Solution
|
- A bettery of 10 V and negligible internal resistance is connected acro...
Text Solution
|
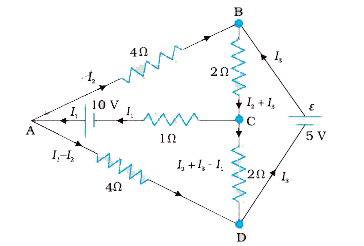
- Determine the current in each brance of the network showin in
Text Solution
|
- The four arma os a Wheatstone bridge have the following resistances: ...
Text Solution
|
- In a meterbridge, the null point is found at a distance of 33.7cm from...
Text Solution
|
- A rsisitance of R Omega draws current from a potentiometer. Te potent...
Text Solution
|