As shown in the figure, AB and CD are two common tangents to circles with centres `O_(1) and O_(2)` and different radius. Prove that AB=CD 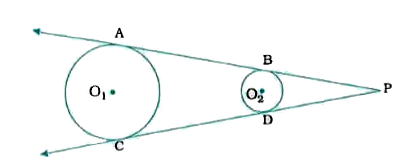
As shown in the figure, AB and CD are two common tangents to circles with centres `O_(1) and O_(2)` and different radius. Prove that AB=CD 

Text Solution
Verified by Experts
Here sources A, B, C, D emit coherent light waves simultaneously with amplitude a, wavelength `lamda` and frequency f. When these waves superpose at point `R_(1)` at time t, displacements of light vectors in them are suppose `y_(A),y_(B),y_(C)andy_(D)` respectively.
Now according to wave equation `y=asin(omegat-kx+phi)` for simplicity assume `(omegat-kx)=theta` and initial phase for source A as `phi=0`. Now
`y_(A)=asin(theta+0)=asintheta" "......(1)`
(ii) Here `BR_(1)-AR_(1)=(lamda)/(2)` and so, at point `R_(1)` at time t, phase of B will be less than phase of A by amount `pi` rad and so,
`y_(B)=asin(theta-pi)=asin{-(pi-theta)}`
`=-asin(pi-theta)`
`:.y_(B)=-asintheta" "....(2)`
Here `CR_(1)-AR_(1)=(lamda)/(2)+(lamda)/(2)=lamda` and so at point `R_(1)`, at time t phase of C is less then phase of A by amount `2pi` rad and so,
`y_(C)=asin(theta-2pi)=asin{-(2pi-theta)}`
`=-asin(2pi-theta)`
`:.y_(C)=-a(-sintheta)=asintheta" "......(3)`
(iv) Here `DR_(1)^(2)=DB^(2)+BR_(1)^(2)`
`=((lamda)/(2))^(2)+d^(2)`
`:.DR_(1)=sqrt(d^(2)+(lamda^(2))/(4))`
Path difference betwen D and A
`=DR_(1)-AR_(1)`
`=DR_(1)-(BR_(1)-AR_(1))`
`=sqrt(d^(2)+(lamda^(2))/(4))-(d-(lamda)/(2))`
`=sqrt(d^(2)+(lamda^(2))/(4))-d+(lamda)/(2)`
`={d^(2)(1+(lamda^(2))/(4d^(2)))}^(1//2)-d+(lamda)/(2)`
`=d(1+(lamda^(2))/(4d^(2)))^(1//2)-d+(lamda)/(2)`
`=d(1+(lamda^(2))/(8d^(2)))-d+(lamda)/(2)`
(Expanding according to binomial theorem and then retaining only first two terms)
`=d(1+0)-d+(lamda)(2)("":.Heredgtgtgtgtlamda)`
`=(lamda)/(2)`
`implies` At point `R_(1)`, at time t, phase of D would be less than phase of A by amount `pi` rad. Hence,
`y_(D)=asin(theta-pi)`
`=asin{-(pi-theta)}`
`=-asin(pi-theta)`
`:.y_(D)=-asintheta" "......(4)`
Now, resultant displacement of light vector at point `R_(1)` at time t,
`y=y_(A)+y_(B)+y_(C)+y_(D)`
`=asintheta-asintheta+asintheta-asintheta`
`:.y=0`
`implies` Now, resultant intensity of light at point `R_(1)`, `I_(R_(1))=0" "....(5)`
Now, let us consider point `R_(2)`,
(i) Path difference between A and B,
`=AR_(2)-BR_(2)`
`=sqrt(d^(2)+(lamda^(2))/(4))-d`
`={d^(2)(1+(lamda^(2))/(4d^(2)))}^(1//2)-d`
`=d(1+(lamda^(2))/(4d^(2)))^(1//2)-d`
`=d(1+(lamda^(2))/(4d^(2)))^(1//2)-d`
`=d+(lamda^(2))/(8d)-d`
`=(lamda^(2))/(8d)`
`~~0" "("":.dgtgtgtgtlamda)`
If, `y._(A)=asintheta` then `y._(A)=asintheta`
( `:.` path differene =0 )
similarly `y._(C)=asintheta`
( `:.` path difference =0)
But `y_(D)=asin(theta-pi)`
( `:.` path difference `=(lamda)/(2)` )
`=asintheta{-(pi-theta)}`
`=-asin(pi-theta)`
`=-asintheta`
Now, resultant displacement of light vector at point `R_(2)` at time t is
`y.=y_(A)+y._(B)+y._(C)+y._(D)`
`=asintheta+asintheta+asintheta-asintheta`
`=2asintheta`
`=2asin(omegat-kx)" "("":.theta=omegat-kx)`
Now, if instantaneous intensity of light at point `R_(2)` at time t is I then,
`1propy.^(2)`
`:.Iprop4a^(2)sin^(2)(omegat-kx)`
`:.I=Kxx4a^(2)sin^(2)(omegat-kx)`
`implies` Average intensity of light in every periodic time) at point `R_(2)` will be,
`:.ltIgt""=Kxx4a^(2)xx(1)/(2)=2Ka^(2)`
`implies` Now, showing above average intensity at point `R_(1)` by symbol `I_(R_(2))`,
`I_(R_(1))=2Ka^(2)" "......(6)`
From equation (5) and (6), `I_(R_(2))gtI_(R_(1))`
If all the sources are switched on at a time then intensity of light at point `R_(2)` will be greater than that at point `R_(1)`.
(ii) Now, when source B is turned off, resultant displacement of light vector at point `R_(1)`,
`y=y_(A)+y_(C)+y_(D)`
`=asintheta+asintheta-asintheta`
(From equations (1), (2), (4))
`=asintheta`
`y=asin(omegat-kx)`
`:.I_(R_(1))=Kxxa^(2)xx(1)/(2)=(Ka^(2))/(2)" "......(7)`
Now, resultant displacement of light vector at point `R_(2)` will be,
`y.=y._(A)+y._(C)+y._(D)`
`:.y.=asintheta+asintheta-asintheta`
`:.y.=asintheta`
`:.y.=asin(omegat-kx)` ,
`:.I_(R_(2))=Kxxa^(2)xx(1)/(2)=(Ka^(2))/(2)" ".....(8)`
From equations (7) and (8) `I_(R_(1))=I_(R_(2))" "......(9)`
When source B is turned off, intensities of light at points `R_(1)` and `R_(2)` would be equal.
(iii) Now, when source D is turned off, resultan displacement of light vector at point `R_(1)` is
`y=y_(A)+y_(B)+y_(C)`
`:.y=asintheta-asintheta+asintheta`
(From equations (1), (2), (3))
`:.y=asintheta`
`:.y=asin(omegat-kx)`
`:.I_(R_(1))=Kxxa^(2)xx(1)/(2)=(Ka^(2))/(2)" "......(10)`
Here, resultant displacement of light vector at point `R_(2)` will be
`y.=y._(A)+y._(B)+y._(C)`
`:.y.=asintheta+asintheta+asintheta`
`:.y.=3asintheta`
`:.y.=3asin(omegat-kx)`
`:.I_(R_(2))=Kxx9a^(2)xx(1)/(2)=(9Ka^(2))/(2)" ".....(11)`
From equations (10) and (11), `I_(R_(2))gtI_(R_(1))`
Intensity of light at point `R_(2)` will be greater than that at point `R_(1)`.
(iv) Here, whether we turn off B or we turn off D in both the cases same intensity of light is obtained at point `R_(1)`. Hence receiver `R_(1)` can not differentiate (or can not distinguish) betweeen these two phenomena.
But receiver `R_(2)` can distinguish between these two phenomena because according to equation (6), when all the four sources are turned "on" intensity of light at point `R_(2)` is `2Ka^(2)`. Now, when only B is turned "off", intensity of light at point `R_(2)` decreases and becomes `(1)/(2)Ka^(2)` (as per equation (7) and when only D is turned "off" intensity of light at point `R_(2)`, increases and becomes `(9Ka^(2))/(2)`.
Thus, when intensity of light decreases at point `R_(2)`, it will come to know that source B is turned "off" and when intensity of light increases at point `R_(2)`, it will come to know that source D is turned "off".
Now according to wave equation `y=asin(omegat-kx+phi)` for simplicity assume `(omegat-kx)=theta` and initial phase for source A as `phi=0`. Now
`y_(A)=asin(theta+0)=asintheta" "......(1)`
(ii) Here `BR_(1)-AR_(1)=(lamda)/(2)` and so, at point `R_(1)` at time t, phase of B will be less than phase of A by amount `pi` rad and so,
`y_(B)=asin(theta-pi)=asin{-(pi-theta)}`
`=-asin(pi-theta)`
`:.y_(B)=-asintheta" "....(2)`
Here `CR_(1)-AR_(1)=(lamda)/(2)+(lamda)/(2)=lamda` and so at point `R_(1)`, at time t phase of C is less then phase of A by amount `2pi` rad and so,
`y_(C)=asin(theta-2pi)=asin{-(2pi-theta)}`
`=-asin(2pi-theta)`
`:.y_(C)=-a(-sintheta)=asintheta" "......(3)`
(iv) Here `DR_(1)^(2)=DB^(2)+BR_(1)^(2)`
`=((lamda)/(2))^(2)+d^(2)`
`:.DR_(1)=sqrt(d^(2)+(lamda^(2))/(4))`
Path difference betwen D and A
`=DR_(1)-AR_(1)`
`=DR_(1)-(BR_(1)-AR_(1))`
`=sqrt(d^(2)+(lamda^(2))/(4))-(d-(lamda)/(2))`
`=sqrt(d^(2)+(lamda^(2))/(4))-d+(lamda)/(2)`
`={d^(2)(1+(lamda^(2))/(4d^(2)))}^(1//2)-d+(lamda)/(2)`
`=d(1+(lamda^(2))/(4d^(2)))^(1//2)-d+(lamda)/(2)`
`=d(1+(lamda^(2))/(8d^(2)))-d+(lamda)/(2)`
(Expanding according to binomial theorem and then retaining only first two terms)
`=d(1+0)-d+(lamda)(2)("":.Heredgtgtgtgtlamda)`
`=(lamda)/(2)`
`implies` At point `R_(1)`, at time t, phase of D would be less than phase of A by amount `pi` rad. Hence,
`y_(D)=asin(theta-pi)`
`=asin{-(pi-theta)}`
`=-asin(pi-theta)`
`:.y_(D)=-asintheta" "......(4)`
Now, resultant displacement of light vector at point `R_(1)` at time t,
`y=y_(A)+y_(B)+y_(C)+y_(D)`
`=asintheta-asintheta+asintheta-asintheta`
`:.y=0`
`implies` Now, resultant intensity of light at point `R_(1)`, `I_(R_(1))=0" "....(5)`
Now, let us consider point `R_(2)`,
(i) Path difference between A and B,
`=AR_(2)-BR_(2)`
`=sqrt(d^(2)+(lamda^(2))/(4))-d`
`={d^(2)(1+(lamda^(2))/(4d^(2)))}^(1//2)-d`
`=d(1+(lamda^(2))/(4d^(2)))^(1//2)-d`
`=d(1+(lamda^(2))/(4d^(2)))^(1//2)-d`
`=d+(lamda^(2))/(8d)-d`
`=(lamda^(2))/(8d)`
`~~0" "("":.dgtgtgtgtlamda)`
If, `y._(A)=asintheta` then `y._(A)=asintheta`
( `:.` path differene =0 )
similarly `y._(C)=asintheta`
( `:.` path difference =0)
But `y_(D)=asin(theta-pi)`
( `:.` path difference `=(lamda)/(2)` )
`=asintheta{-(pi-theta)}`
`=-asin(pi-theta)`
`=-asintheta`
Now, resultant displacement of light vector at point `R_(2)` at time t is
`y.=y_(A)+y._(B)+y._(C)+y._(D)`
`=asintheta+asintheta+asintheta-asintheta`
`=2asintheta`
`=2asin(omegat-kx)" "("":.theta=omegat-kx)`
Now, if instantaneous intensity of light at point `R_(2)` at time t is I then,
`1propy.^(2)`
`:.Iprop4a^(2)sin^(2)(omegat-kx)`
`:.I=Kxx4a^(2)sin^(2)(omegat-kx)`
`implies` Average intensity of light in every periodic time) at point `R_(2)` will be,
`:.ltIgt""=Kxx4a^(2)xx(1)/(2)=2Ka^(2)`
`implies` Now, showing above average intensity at point `R_(1)` by symbol `I_(R_(2))`,
`I_(R_(1))=2Ka^(2)" "......(6)`
From equation (5) and (6), `I_(R_(2))gtI_(R_(1))`
If all the sources are switched on at a time then intensity of light at point `R_(2)` will be greater than that at point `R_(1)`.
(ii) Now, when source B is turned off, resultant displacement of light vector at point `R_(1)`,
`y=y_(A)+y_(C)+y_(D)`
`=asintheta+asintheta-asintheta`
(From equations (1), (2), (4))
`=asintheta`
`y=asin(omegat-kx)`
`:.I_(R_(1))=Kxxa^(2)xx(1)/(2)=(Ka^(2))/(2)" "......(7)`
Now, resultant displacement of light vector at point `R_(2)` will be,
`y.=y._(A)+y._(C)+y._(D)`
`:.y.=asintheta+asintheta-asintheta`
`:.y.=asintheta`
`:.y.=asin(omegat-kx)` ,
`:.I_(R_(2))=Kxxa^(2)xx(1)/(2)=(Ka^(2))/(2)" ".....(8)`
From equations (7) and (8) `I_(R_(1))=I_(R_(2))" "......(9)`
When source B is turned off, intensities of light at points `R_(1)` and `R_(2)` would be equal.
(iii) Now, when source D is turned off, resultan displacement of light vector at point `R_(1)` is
`y=y_(A)+y_(B)+y_(C)`
`:.y=asintheta-asintheta+asintheta`
(From equations (1), (2), (3))
`:.y=asintheta`
`:.y=asin(omegat-kx)`
`:.I_(R_(1))=Kxxa^(2)xx(1)/(2)=(Ka^(2))/(2)" "......(10)`
Here, resultant displacement of light vector at point `R_(2)` will be
`y.=y._(A)+y._(B)+y._(C)`
`:.y.=asintheta+asintheta+asintheta`
`:.y.=3asintheta`
`:.y.=3asin(omegat-kx)`
`:.I_(R_(2))=Kxx9a^(2)xx(1)/(2)=(9Ka^(2))/(2)" ".....(11)`
From equations (10) and (11), `I_(R_(2))gtI_(R_(1))`
Intensity of light at point `R_(2)` will be greater than that at point `R_(1)`.
(iv) Here, whether we turn off B or we turn off D in both the cases same intensity of light is obtained at point `R_(1)`. Hence receiver `R_(1)` can not differentiate (or can not distinguish) betweeen these two phenomena.
But receiver `R_(2)` can distinguish between these two phenomena because according to equation (6), when all the four sources are turned "on" intensity of light at point `R_(2)` is `2Ka^(2)`. Now, when only B is turned "off", intensity of light at point `R_(2)` decreases and becomes `(1)/(2)Ka^(2)` (as per equation (7) and when only D is turned "off" intensity of light at point `R_(2)`, increases and becomes `(9Ka^(2))/(2)`.
Thus, when intensity of light decreases at point `R_(2)`, it will come to know that source B is turned "off" and when intensity of light increases at point `R_(2)`, it will come to know that source D is turned "off".
Topper's Solved these Questions
WAVE OPTICS
KUMAR PRAKASHAN|Exercise SECTION-D (MULTIPLCE CHOICE QUESTIONS (MCQS)) (MCQS FROM DARPAN BASED ON TEXTBOOK)|239 VideosWAVE OPTICS
KUMAR PRAKASHAN|Exercise SECTION-C NCERT Exemplar Solution (Short Answer Type Questions )|3 VideosSEMICONDUCTOR ELECTRONICS : MATERIALS, DEVICES AND SIMPLE CIRCUITS
KUMAR PRAKASHAN|Exercise Section-D : Multiple Choice Questions (MCQs) (MCQs asked in Competitive Exams)|129 Videos
Similar Questions
Explore conceptually related problems
Choose the correct answer and give justification for each. In the figure XY and X^(1)Y^(1) are two parallel tangents to a circle with centre O and another tangent AB with point of contact C intersecting XY at A and X^(1)Y^(1) at B then /_AOB=
In the given figure, AB and CD are two diameters of a circle (with centre O) perpendicular to each other and OD is the diameter of the smaller circle. If OA = 7 cm, find the area of the shaded region.
In the given figure. If TP and TQ are the two tangents to a circle with centre O so that angle POQ= 110^(@) , then angle PTQ is equal to …….
In the figure , if AB = CD and angle AOB - 90^@ find angle COD
If a line intersects two concentric circles (circles with the same centre) with centre O at A,B,C and D), prove that AB= CD
In the given figure, Rq is a tangent to the circle with centre O. if SQ = 6cm and QR = 4cm. Then. OR = ……….cm.
In the adjacent figure, AB is a chord of circle with centre O. CD is the diameter perpendicualr to AB. Show that AD = BD
In the adjacent figure, there are two concentric circles with centre ‘O’. Chord AD of the bigger circle intersects the smaller circle at B and C. Show that AB = CD.
In the given figure AB and CD bisect each other at O. Prove that AC = BD.
KUMAR PRAKASHAN-WAVE OPTICS-SECTION-C NCERT Exemplar Solution (Long Answer Type Questions)
- if the intensity of the principal maximum in the single slit Fraunhoff...
Text Solution
|
- What will be the diffraction angle of first order maxima in diffractio...
Text Solution
|
- As shown in the figure, AB and CD are two common tangents to circles w...
Text Solution
|
- The optical properties of a medium are governed by the relative permit...
Text Solution
|
- To ensure almost 100 per cent transmittivity, photographic lenses are ...
Text Solution
|