Home
Class 12
PHYSICS
A student performs an experiment on phot...


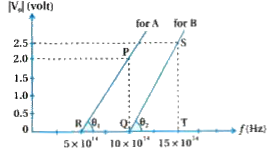
A student performs an experiment on photoelectric effect,using two materials A and B.A plot `V_("stop")vs` v is given in figure.
(i)Which material A or B has a higher work function?
(ii)Given the electric charge of an electron`=1.6xx10^(-19)`C,find the value of the h obtained from the experiment for both A and B.Comment on whether it is consistent with Einstein's theory:

Text Solution

Verified by Experts

(i)Work function ,`phi_(0)=hf_(0)`
(where `f_(0)`=threshold frequency)
`therefore phi_(0)propf_(0)` ……..(1)
From the figure ,
`f_(0)A=5xx10^(14)`Hz
`f_(0)B=10xx10^(14)Hz`
`impliesf_(0)Bgtf_(0)A`
`implies` From relation(1),
`phi_(0)Bgtphi_(0)A`
(ii)We know that slope of graph of |`V_(0)|tof`
Gives us value of `((h)/(e))`.Hence
Slope of graph for A,
`tantheta_(1)=(PQ)/(QR)`
`therefore (h)/(e)=(2)/(5xx10^(14))=0.4xx10^(-14)`
`therefore h=0.4xx10^(-14)xxe`
`therefore h=0.4xx10^(-14)xx1.6xx10^(-19)`
`therefore h=6.4xx10^(-34)Js` .......(2)
Slope of graph for B,
`tantheta_(2)=(ST)/(QT)`
`therefore (h)/(e)=(2.5)/(5xx10^(14))=0.5xx10^(14)`
`therefore h=0.5xx10^(-14)xxe`
`=0.5xx10^(-14)xx1.6xx10^(19)`
`h=8xx10^(-34)Js` ..........(3)
Thus ,here value of h are obtained different from the graphs for A and B.Hence ,above experimental observations are not consistent with Einstein.s theory.
Promotional Banner

Topper's Solved these Questions

  • DUAL NATURE OF RADIATION AND MATTER

    KUMAR PRAKASHAN|Exercise Section-D (multiple choice questions (MCQs)|48 Videos

  • DUAL NATURE OF RADIATION AND MATTER

    KUMAR PRAKASHAN|Exercise Section-D (multiple choice questions (MCQs) (photo-electric effect)|1 Videos

  • DUAL NATURE OF RADIATION AND MATTER

    KUMAR PRAKASHAN|Exercise Section-C (Very short answer type questions)|11 Videos

  • CURRENT ELECTRICITY

    KUMAR PRAKASHAN|Exercise SECTION [D] MULTIPLE CHOICE QUESTIONS (MCQs) (MCQs ASKED IN BOARD EXAM AND GUJCET)|23 Videos

  • ELECTRIC CHARGES AND FIELDS

    KUMAR PRAKASHAN|Exercise SECTION D MCQS ASKED IN COMPETITIVE EXAMES (MCQS AKSED IN BOARD EXAM AND GUJCET)|14 Videos

Similar Questions

Explore conceptually related problems

A student performs an experiment to determine how the range of a ball depends on the velocity with which it is projected. The "range" is the distance between the points where the ball lends and from where it was projected, assuming it lands at the same height from which it was projected. It each trial, the student uses the same baseball, and launches it at the same angle. Table shows the experimental results. |{:("Trail","Launch speed" (m//s),"Range"(m)),(1,10,8),(2,20,31.8),(3,30,70.7),(4,40,122.5):}| Based on this data, the student then hypothesizes that the range, R, depends on the initial speed v_(0) according to the following equation : R=Cv_(0)^(n) , where C is a constant and n is another constant. The student speculates that the constant C depends on :- (i) The angle at which the ball was launched (ii) The ball's mass (iii) The ball's diameter If we neglect air resistance, then C actually depends on :-

Two metallic plate A and B , each of area 5 xx 10^(-4)m^(2) , are placed parallel to each at a separation of 1 cm plate B carries a positive charge of 33.7 xx 10^(-12) C A monocharonatic beam of light , with photoes of energy 5 eV each , starts falling on plate A at t = 0 so that 10^(16) photons fall on it per square meter per second. Assume that one photoelectron is emitted for every 10^(6) incident photons fall on it per square meter per second. Also assume that all the emitted photoelectrons are collected by plate B and the work function of plate A remain constant at the value 2 eV Determine (a) the number of photoelectrons emitted up to i = 10s, (b) the magnitude of the electron field between the plate A and B at i = 10 s, and (c ) the kinetic energy of the most energotic photoelectrons emitted at i = 10 s whenit reaches plate B Negilect the time taken by the photoelectrons to reach plate B Take epsilon_(0) = 8.85 xx 10^(-12)C^(2)N- m^(2)

A mercury lamp is a convenient source for studying frequency dependence of photoelectric emission, since it gives a number of spectral lines ranging from the Uv to the red end of the visible spectrum. In our experiment with rubidium photo-cell, the following lines from a mercury source were used: lambda_(1) = 3650 Å, lambda_(2) = 4047 Å, lambda_(3) = 4358 Å, lambda_(4) = 5461 Å, lambda_(5) = 6907 Å , The stopping voltages, respectively, were measured to be: V_(01) = 1.28 V, V_(02) = 0.95 V, V_(03) = 0.74 V, V_(04) = 0.16 V, V_(05) = 0 V Determine the value of Planck’s constant h, the threshold frequency and work function for the material. [Note: You will notice that to get h from the data, you will need to know e (which you can take to be 1.6 xx 10^(-19) C ). Experiments of this kind on Na, Li, K, etc. were performed by Millikan, who, using his own value of e (from the oil-drop experiment) confirmed Einstein’s photoelectric equation and at the same time gave an independent estimate of the value of h.]

(a) Estimate the speed with which electrons emitted from a heated emitter of an evacuated tube impinge on the collector maintained at a potential difference of 500 V with respect to the emitter. Ignore the small initial speeds of the electrons. The specific charge of the electron, i.e., its e/m is given to be 1.76 xx 10^(11) C kg^(-1) . (b) Use the same formula you employ in (a) to obtain electron speed for an collector potential of 10 MV. Do you see what is wrong ? In what way is the formula to be modified?

(a) Estimate the speed with which electrons emitted from a heated emitter of an evacuated tube impinge on the collector maintained at a potential difference of 500 V with respect to the emitter.Ignore the small initial speeds of the electrons.The specific charge of the electron ,i.e., its (e)/(m) is given to be 1.76xx10^(11)Ckg^(-1) (b) Use the same formula you employ in (a)to obtain electron speed for an collector potential of 10 MV.Do you see what is wrong ?in what way is the formula to be modified?

The graph between 1/lambda and stopping potential V_(0) of two metals having work funcation phi_(1) and phi_(2) in an experiment of photoelectric effect is obtained as shown in the figure. Find out - (i) Threshold wavelength of both metals (ii) phi_(1) : phi_(2) (iii) Which metal can emit photoelectrons with visible light ?

A physical quantity is a phyical property of a phenomenon , body, or substance , that can be quantified by measurement. The magnitude of the components of a vector are to be considered dimensionally distinct. For example , rather than an undifferentiated length unit L, we may represent length in the x direction as L_(x) , and so forth. This requirement status ultimately from the requirement that each component of a physically meaningful equation (scaler or vector) must be dimensionally consistent . As as example , suppose we wish to calculate the drift S of a swimmer crossing a river flowing with velocity V_(x) and of widht D and he is swimming in direction perpendicular to the river flow with velocity V_(y) relation to river, assuming no use of directed lengths, the quantities of interest are then V_(x),V_(y) both dimensioned as (L)/(T) , S the drift and D width of river both having dimension L. with these four quantities, we may conclude tha the equation for the drift S may be written : S prop V_(x)^(a)V_(y)^(b)D^(c) Or dimensionally L=((L)/(T))^(a+b)xx(L)^(c) from which we may deduce that a+b+c=1 and a+b=0, which leaves one of these exponents undetermined. If, however, we use directed length dimensions, then V_(x) will be dimensioned as (L_(x))/(T), V_(y) as (L_(y))/(T), S as L_(x)" and " D as L_(y) . The dimensional equation becomes : L_(x)=((L_(x))/(T))^(a) ((L_(y))/(T))^(b)(L_(y))^(c) and we may solve completely as a=1,b=-1 and c=1. The increase in deductive power gained by the use of directed length dimensions is apparent. A conveyer belt of width D is moving along x-axis with velocity V. A man moving with velocity U on the belt in the direction perpedicular to the belt's velocity with respect to belt want to cross the belt. The correct expression for the drift (S) suffered by man is given by (k is numerical costant )

Snell's law relation for air glass boundary is given by equation n_(air) sin theta_(1) = n_(glass) sin theta_(r) . Here angle of refraction in glass is theta_(r) and the angle of incident in air is theta_(i) . The refractive index of air is n_(air)=1 (with negligible uncertainty). In an experiment to verify Snell's the best fit line on a graph between sin theta_(r) (on the y-axis) and sin theta_(i) (on the x-axis) is given by the eqyuation y=(6.66pm0.05)xx10^(-1)x+(0.022pm0.024) . The refractive index of the glass, including the error is reported as 1.abpm 0.0c , where a,b and c are digits after tje decimal point. Calculate value of (a+b-c) .

Two parallel beams of light P and Q (separation d) containing radiations of wavelengts 4000Å and 5000 Å (which are mutually coherent in each wavelength separately) are incident normally on a prism as shown in figure the refractive index of the prism as a function of wavelength is given by the relation mu(lamda)=1.20+(b)/(lamda^(2)) where lamda is in Å and b is a positive constant. The value of b is such that the condition for total reflection at the face AC is just satisfied for one wavelength and is not satisfied for the other. A convergent lens is used to bring these transmitted beams into focus. If the intensities of the upper and the lower beams immediately after transmission from the face AC, are 4I and I respectively, find the resultant intensity at the focus.

A point source is emitting 0.2 W of ultravio- let radiation at a wavelength of lambda = 2537 Å . This source is placed at a distance of 1.0 m from the cathode of a photoelectric cell. The cathode is made of potassium (Work function = 2.22 eV ) and has a surface area of 4 cm^(2) . (a) According to classical theory, what time of exposure to the radiation shall be required for a potassium atom to accumulate sufficient energy to eject a photoelectron. Assume that radius of each potassium atom is 2 Å and it absorbs all energy incident on it. (b) Photon flux is defined as number of light photons reaching the cathode in unit time. Calculate the photon flux. (c) Photo efficiency is defined as probability of a photon being successful in knocking out an electron from the metal surface. Calculate the saturation photocurrent in the cell assuming a photo efficiency of 0.1. (d) Find the cut – off potential difference for the cell.