Similar Questions
Explore conceptually related problems
Recommended Questions
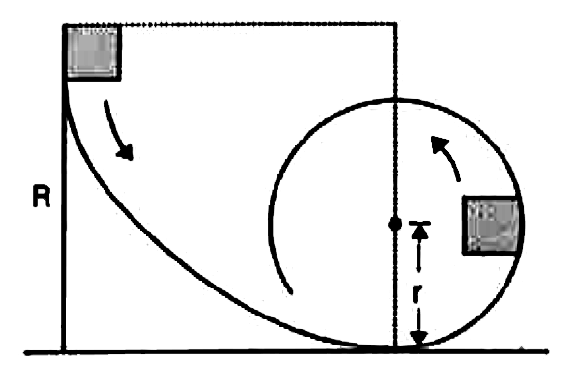
- A small block of mass m slides along a frictionless loop-the-loop (loo...
Text Solution
|
- Two different wire loops are concentric and lie in the same plane. The...
Text Solution
|
- Two different wire loops are concentric and lie in the same plane. The...
Text Solution
|
- A small of mass m starts from rest at the position shown and slides al...
Text Solution
|
- A small block of mass m slides along a frictionless loop-the-loop (loo...
Text Solution
|
- A small object of mass m starts from rest at the position shown and sl...
Text Solution
|
- A small circular loop of wire of radius a is located at the centre of ...
Text Solution
|
- R त्रिज्या के किसी ऊर्ध्वाधर पाश ( लूप ) में m द्रव्यमान के किसी पिंड...
Text Solution
|
- A small circular loop of wire of radius a is located at the centre of ...
Text Solution
|