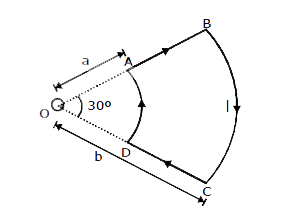
The magnitude of the magnetic field (B) due to loop ABCD at the origin (O) is

A current loop ABCD is held fixed on the plane of the paper as shown in figure. The arcs BC( radius = b) and DA ( radius = a) of the loop are joined by two straight wires AB and CD at the origin O is 30^(@) . Another straight thin wire with steady current I_(1) flowing out of the plane of the paper is kept at the origin . The magnitude of the magnetic field (B) due to the loop ABCD at the origin (o) is :

The magnitude of the magnetic filed B due to the loop ABCD at origin (O) is

A current - carrying loop is shown in the figure. The magnitude of the magnetic field produced at a point O is

A current - carrying loop is shown in the figure. The magnitude of the magnetic field produced at a point O is

Find the magnitude of the magnetic field at the origin O due to very long conductor carrying current I of the shape as shown in figure.

A cell is connected between the points A and C of a circular conductor ABCD of centre 'O'.angle AOC = 60^(@) . If B_(​1) and B_(​2) are the magnitudes of the magnetic fields at O due to the currents in ABC and ADC respectively, the ratio (B_(1))/(B_(2)) , is

A cell is connected between the points A and C of a circular conductor ABCD of centre O*/_AOC=60^@ . If B_1 and B_2 are the magnitudes of the magnetic fields at O due to the currents in ABC and ADC respectively, the ratio B_1//B_2 is

A cell is connected between the points A and C of a circular conductor ABCD of centre 'O'.angle AOC = 60^(@) . If B_(​1) and B_(​2) are the magnitudes of the magnetic fields at O due to the currents in ABC and ADC respectively, the ratio (B_(1))/(B_(2)) , is

A cell is connected between the points A and C of a circular conductor ABCD of centre O . angle AOC = 60^(@) . If B_(​1) and B_(​2) are the magnitudes of the magnetic fields at O due to the currents in ABC and ADC respectively, the ratio (B_(1))/(B_(2)) , is