Similar Questions
Explore conceptually related problems
Recommended Questions
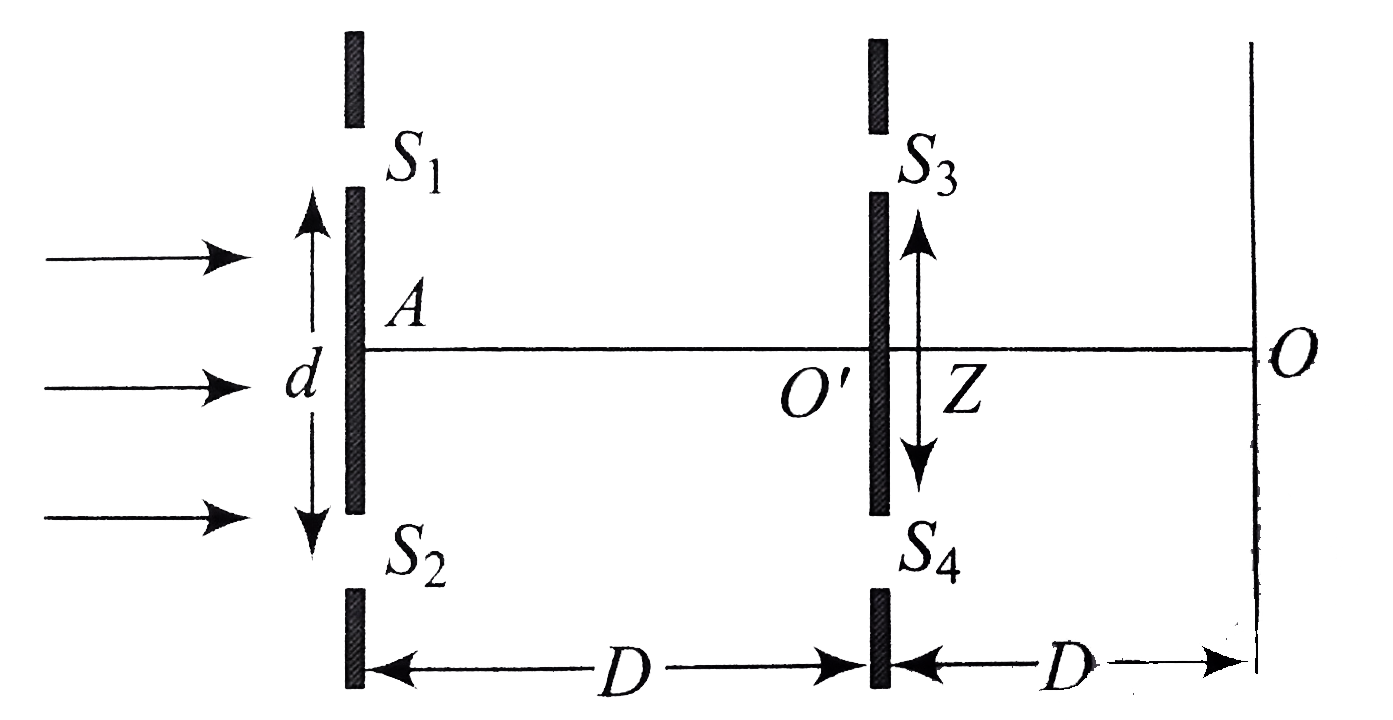
- In the arrangement shown in Fig., slits S(1) and S(4)are having a vari...
Text Solution
|
- In the arrangement shown in figure, light of wavelength 6000 Å is inci...
Text Solution
|
- In the arrangement shown in figure, light of wavelength 6000 Å is inci...
Text Solution
|
- Consider the situation shown in fig. The two slits S(1) and S(2) place...
Text Solution
|
- Consider the situation shown in fig. The two slits S(1) and S(2) place...
Text Solution
|
- In the arrangement shown in Fig., slits S(1) and S(4)are having a vari...
Text Solution
|
- In the arrangement shown in Fig., slits S(1) and S(4) are having a var...
Text Solution
|
- In the arrangement shown in Fig., slits S(1) and S(4) are having a var...
Text Solution
|
- In arrangement shown in figure, plane wavefront of monochromatic light...
Text Solution
|