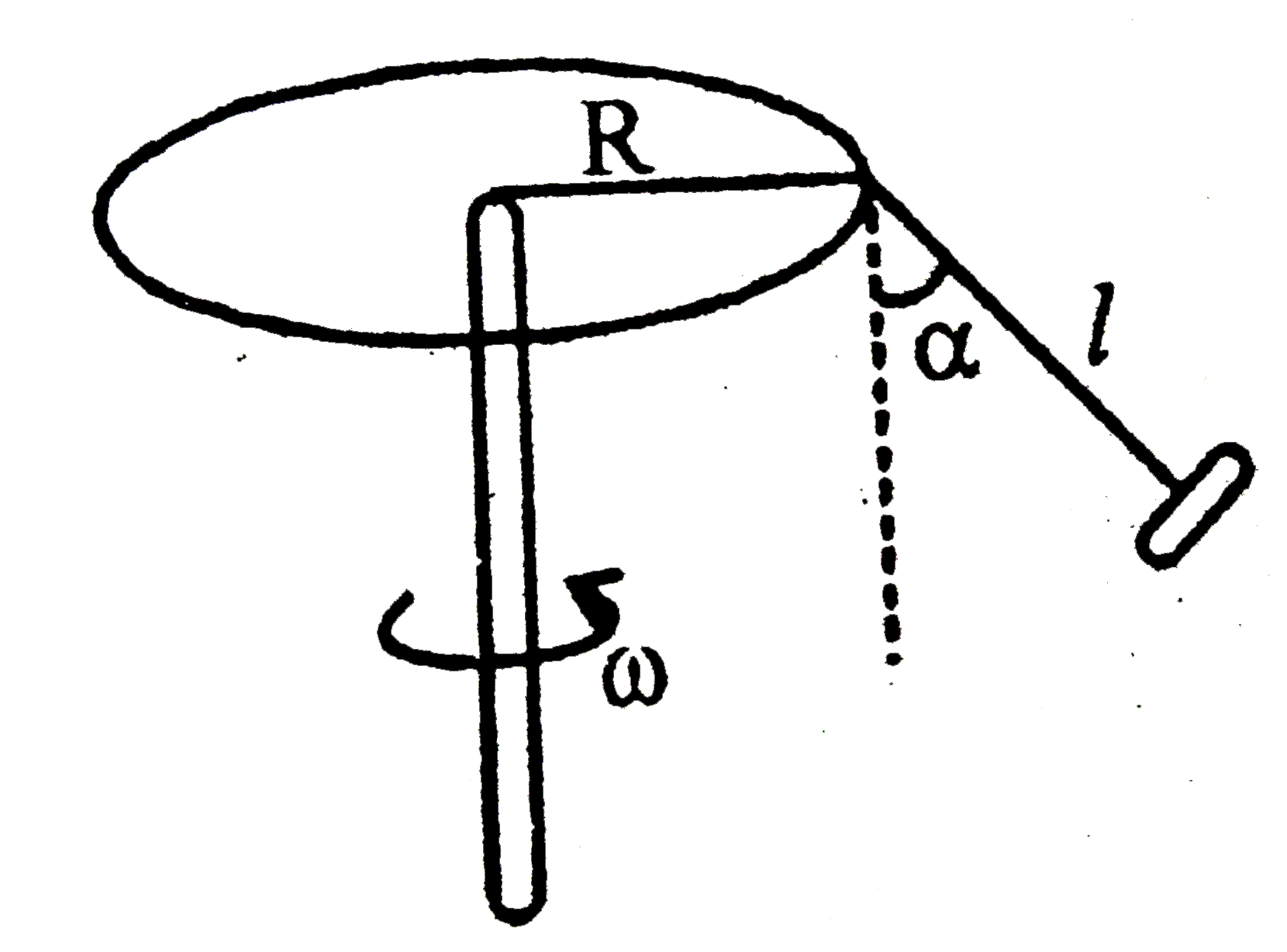Similar Questions
Explore conceptually related problems
Recommended Questions
- With what angular velocity omega (in rad/s) should we rotate the disc ...
Text Solution
|
- A disc of radius R has a light pole fixed perpendicular to the disc at...
Text Solution
|
- With what angular velocity omega (in rad/s) should we rotate the disc ...
Text Solution
|
- A disc of mass 2 kg and radius 0.2 m is rotating with angular velocity...
Text Solution
|
- A disc of mass 1 kg and radius 0.1 m is rotating with angular velocity...
Text Solution
|
- A disc has mass 'M' and radius 'R'. How much tangential force should b...
Text Solution
|
- A large disc has mass 2kg and radius 0.2 m and initial angular velocit...
Text Solution
|
- A disc of mass 2 kg and radius 0.2 m is rotating with angular veocity ...
Text Solution
|
- A circular disc of mass M and radius R is rotating with angular veloci...
Text Solution
|