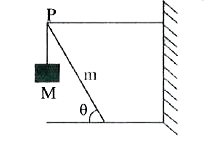
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
FRICTION
AAKASH SERIES|Exercise ADDITIONAL PRACTICE EXERCISE PRACTICE SHEET (ADVANCED) (MORE THAN ONE CORRECT ANSWER TYPE QUESTIONS)|1 VideosFRICTION
AAKASH SERIES|Exercise ADDITIONAL PRACTICE EXERCISE (LELVL-II) (LECTURE SHEET (ADVANCED)) (LINKED COMPREHENSION TYPE QUESTIONS)|2 VideosFLUID MECHANICS
AAKASH SERIES|Exercise Questions for Descriptive Answers|14 VideosGAUSS.S LAW
AAKASH SERIES|Exercise PROBLEMS (LEVEL - II)|12 Videos
Similar Questions
Explore conceptually related problems
AAKASH SERIES-FRICTION -ADDITIONAL PRACTICE EXERCISE PRACTICE SHEET (ADVANCED) (STRAIGHT OBJECTIVE TYPE QUESTIONS)
- A body is sliding down a rough inclined plane of angle of inclination ...
Text Solution
|
- A block of mass m is placed on a wedge of mass M. Coefficient of frict...
Text Solution
|
- Two blocks M(1) and M(2) rest upon each other on an inclined plane. Co...
Text Solution
|
- If coefficient of friction between all surfaces is 0.4, then the minim...
Text Solution
|
- A uniform beam of mass m is inclined at an angletheta to the horizonta...
Text Solution
|